BOAS
- 546
- 19
Hello,
I am confused about a problem regarding work done and pulleys. I am confused mainly by the last two, but not 100% confident in the first two either.
1. Homework Statement
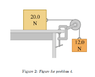
Two blocks are connected by a very light string passing over a massless and frictionless
pulley (Figure 2). The 20.0 N block moves 75.0 cm to the right and the 12.0 N block moves
75.0 cm downward.
(image attached)
Find the work done on
(a) the 20.0 N block if there is no friction between the table and the 20.0 N block.
(b) the 12.0 N block if there is no friction between the table and the 20.0 N block.
(c) the 20.0 N block if µs=0.500 and µk=0.325 between the table and the 20.0 N block.
(d) the 12.0 N block if µs=0.500 and µk=0.325 between the table and the 20.0 N block.
For case (a) the force that is moving the 20.0N block is the weight of the 12.0N block. The work done on the 20.0N block is therefore F x d = 12 x 0.75 = 9 Nm
For case (b) I think I can find the work done by finding the change in gravitational potential energy of the 12.0N block which is mgΔh = -9 Nm.
I think this is correct, to expect the net work done to be 0, since there is no friction which is non-conservative.
However, for question (c), I am confused about using the coefficient of static friction.
The 20N box will move if the static friction force is less than 12N. μn= 10N so the net force in the x direction is 2N.
Now I know the box will move, but is this information relevant to the rest of the question?
The kinetic friction force comes to be f_{k} = \mu_{k} N = 6.5N, so the net force when the box is moving is 5.5N, and thus the work done on the 20N box is w = f x d 4.125N.
I think the work done on the 12N box is still -9Nm because it's change in GPE is still the same, it just changes more slowly.
I know this is a bit of a ramble, but i'd really appreciate it if you could confirm whether my thoughts make sense.
Thanks!
I am confused about a problem regarding work done and pulleys. I am confused mainly by the last two, but not 100% confident in the first two either.
1. Homework Statement
Two blocks are connected by a very light string passing over a massless and frictionless
pulley (Figure 2). The 20.0 N block moves 75.0 cm to the right and the 12.0 N block moves
75.0 cm downward.
(image attached)
Find the work done on
(a) the 20.0 N block if there is no friction between the table and the 20.0 N block.
(b) the 12.0 N block if there is no friction between the table and the 20.0 N block.
(c) the 20.0 N block if µs=0.500 and µk=0.325 between the table and the 20.0 N block.
(d) the 12.0 N block if µs=0.500 and µk=0.325 between the table and the 20.0 N block.
Homework Equations
The Attempt at a Solution
For case (a) the force that is moving the 20.0N block is the weight of the 12.0N block. The work done on the 20.0N block is therefore F x d = 12 x 0.75 = 9 Nm
For case (b) I think I can find the work done by finding the change in gravitational potential energy of the 12.0N block which is mgΔh = -9 Nm.
I think this is correct, to expect the net work done to be 0, since there is no friction which is non-conservative.
However, for question (c), I am confused about using the coefficient of static friction.
The 20N box will move if the static friction force is less than 12N. μn= 10N so the net force in the x direction is 2N.
Now I know the box will move, but is this information relevant to the rest of the question?
The kinetic friction force comes to be f_{k} = \mu_{k} N = 6.5N, so the net force when the box is moving is 5.5N, and thus the work done on the 20N box is w = f x d 4.125N.
I think the work done on the 12N box is still -9Nm because it's change in GPE is still the same, it just changes more slowly.
I know this is a bit of a ramble, but i'd really appreciate it if you could confirm whether my thoughts make sense.
Thanks!