Confusion about the direction of the vectors: motional EMF

[Granger]

Homework Statement

I'm working through an example with motional EMF and I'm having trouble understanding the directions of vectors so that I can apply induction law.

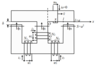
The magnetic circuit seems complex because the circuit is used to analyze other situations but the air gap 3, the coil 3 and the single open loop coil are the ones relevant to this.
We neglect dispersion and the magnetic reluctance of iron.
Section S of the circuit is constant and it's a square of side a.
The air gaps have thickness $\delta$.
All of the coils have the same number of turns.
The open coil has a current $i_0$ that is zero.

[1]: https://i.stack.imgur.com/cE1qK.png

Now we have i2=1A and i3=i0=0 which originates a flux $\phi=-1mH$ and $B_3=-0.625 T$.

Homework Equations

3. The Attempt at a Solution [/B]

Now my question is about the next paragraph:

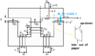
"The motional induction electric field only exists when the coil 0 passes the air gap 3 (I understand that, because only there B is not zero). On that conditions, the elecric field as an orthogonal direction to the figure plan, the same as the current i0 (I think I can also see that...). At the bottom side of the coil we will have $u_0=Bva$ (now that is what I don't understand, what is the direction of B? Is it the same as v? Why? I can't see the direction of the vectors!)."

Basically my question is about the direction of the vectors while applying the induction law.
Can someone help me clarify it? I only need a small draw or some brief explanation.

 

[Merlin3189]

Now we have i2=1A and i3=i0=0 which originates a flux $\phi=-1mH$ and $B_3=-0.625 T$.

"The motional induction electric field only exists when the coil 0 passes the air gap 3 (I understand that, because only there B is not zero). On that conditions, the elecric field as an orthogonal direction to the figure plan, the same as the current i0 (I think I can also see that...). At the bottom side of the coil we will have $u_0=Bva$ (now that is what I don't understand, what is the direction of B? Is it the same as v? Why? I can't see the direction of the vectors!)."

Basically my question is about the direction of the vectors while applying the induction law.
Can someone help me clarify it? I only need a small draw or some brief explanation.

v is shown, left to right on the page; Φ₃ is shown bottom to top of the page; Both in the plane of the page.
The emf must be perpendicular to both and hence to the page, as matches the wire direction, although this is only implied by the 2-D drawing.

The diagram seems to me to imply we are looking at a cross section or maybe a projection of the iron.
It looks as if i₂ flowing through N₂ causes a flux Φ₂ shown pointing upwards, as you'd expect.
The flux is presumably largely confined to the iron, except at the gaps. The flux that reaches the gap on the right is in the opposite sense to the Φ₃ arrow - ie. from top to bottom. Hence, I think the negative sign here.

I would assume that Φ23/SUB] = B_3 a²

 

[rude man]

.

Let's take just a simple "C" iron core, cross-section area = A, with a gap d. There are N turns of wire wound around any part of the "C" except along the gap.
This is a magnetic circuit behaving very much like an electric one:
i <> φ ampere <> weber
emf <> mmf volt <> ampere-turns
voltage <> magnetic potential difference mpd = reluctance x flux <> Ohm's law in electricity
(`you should appreciate the difference between mmf and mpd. It's analogous to the difference between emf and voltage).
current density <> B or amps/m² <> tesla
resistance <> reluctance = ∫dl/μA with l = length of path increment.

A law similar to Kirchoff also existes: mmf = Σ mpd.

A current i through the winding generates an mmf = Ni. The direction of the B field is given by the right-hand rule.This tells you the direction of B and thus of φ. Ther rest is just doing circuit analysis just as in electricity. The core is the wire (assume infinite μ) and the gap is the resistor; the winding is the battery. Etc. Of course it's understood that B fields cannot be confined to a magnetic path the way current can be in a wire so all computations are approximate.

I have no idea how much of the above you are familiar with so my apologies if I went overboard with the rudimentary. I wonder though about your equating Henries with flux as you did: " ... which originates a flux $\phi=-1mH$ ... ". Actually, H = flux/current.