Conical Pendulum with varying string length

[Adrian Simons]

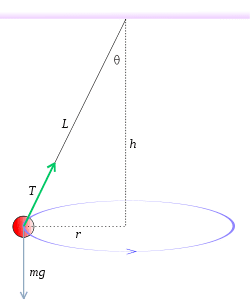
Consider a conical pendulum like that shown in the figure. A ball of mass, m, attached to a string of length, L, is rotating in a circle of radius, r, with angular velocity, ω. The faster we spin the ball (i.e., the greater the ω), the greater the angle, θ, will be, and thus, the smaller the height, h will be.

But now imagine that instead of suspending the ball from a string, we use something like a rubber band that can stretch. Then the faster and faster we spin the ball, the more the rubber band stretches. So we expect L will increase, θ will increase, and h will decrease.

Now let's take a set of different rubber bands. The original lengths of all the rubber bands, with the mass, m, suspended from them vertically, are all identical. However, with a given amount of force, each rubber band stretches a different amount. In other words, say we can model a rubber band as if it were a spring. Then different rubber bands have different spring constants. But remember that they all have the same length, L, when the mass, m, is suspended vertically, before anything starts to spin.

So why is it that regardless of which rubber band you use, as long as you keep ω the same, h remains the same? I mean I worked out the equations and found this to be true. However, I found it to be an unexpected result. Can anybody give me some intuitive insight as to why this should be so?

By the way, this is totally independent of exactly what the nature of the force is that the rubber band exerts, as long as the force is a function of the amount the rubber band stretches.

 

[A.T.]

So why is it that regardless of which rubber band you use, as long as you keep ω the same, h remains the same? I mean I worked out the equations and found this to be true. However, I found it to be an unexpected result. Can anybody give me some intuitive insight as to why this should be so?

Consider the constraints for steady state at different r:
- the vertical component of T is constant
- the horizontal component of T is proportional to r
This is exactly what you get, if h is held constant.

 

[wrobel]

There are a lot of unexpected things. For example, imagine that you have a ring in the vertical plane. Take any point A on the ring and connect this point with the lowest point O by a thin smooth pipe OA. Put a small ball into the pipe at the end A. The ball will roll down to the point O inside the pipe . The time of rolling down does not depend on which point A on the ring you take.

 

[sophiecentaur]

Can anybody give me some intuitive insight as to why this should be so?

I always try to find an Energy Based argument for this sort of question. In the steady state, energy stored due to the modulus of the elastic is not relevant and you can replace it with a string.
The gravitational Potential Energy will be mg(L-h) and the Kinetic Energy will be L m sin(θ)ω²/2.I equated the two and expressed it all in terms of L,θ and ω and ended up with:
Lω² = 2gL(1-cosθ)/cosθ and the L cancels out on either side and the angle is just a function of the angular velocity.

I think that's ok but the usual caveats apply with my algebra.

Alternatively, you can replace a conical pendulum with two superimposed plane pendulums in phase quadrature and in orthogonal planes. The Energy of each individual pendulum will be exchanging KE and PE during their cycles and the sums of the KEs and PEs will be constant.