- #1
aerograce
- 64
- 1
I am pretty confused about how to write Navier-Stokes Equation into conservation form, it seems that from my notes,
first, the density term with the pressure gradient dropped out.
and second, du^2/dx seems to be equal to udu/dx.
Why is it so? I attached my notes here for your reference.

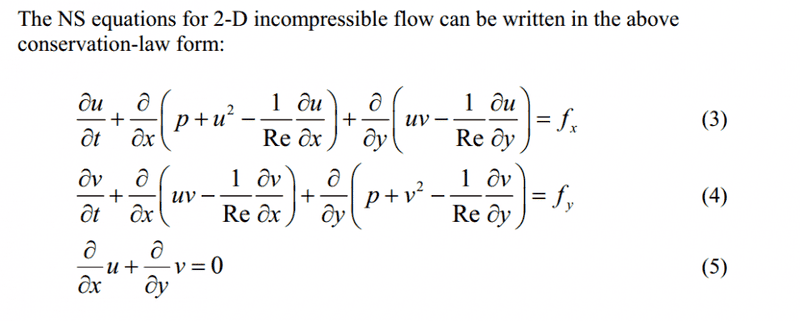
first, the density term with the pressure gradient dropped out.
and second, du^2/dx seems to be equal to udu/dx.
Why is it so? I attached my notes here for your reference.