Conservation of Energy, PE & KE, ball attach to string problem?

[nchin]

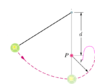
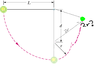
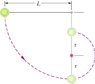
The string in the Figure is L = 120 cm long, has a ball attached to one end, and is fixed at its other end. The distance d to the fixed peg at point P is 75.0 cm. When the initially stationary ball is released with the string horizontal as shown, it will swing along the dashed arc. What is its speed when it reaches (a) its lowest point and (b) its highest point after the string catches on the peg?

Picture of figure:

http://panda.unm.edu/Courses/Price/Phys160/F17-1.jpeg

a) I understand part a

i just use v = sqrt (2gh) = sqrt (2(9.8)(1.20m)) = 4.85 m/s.

b) I found the solution for part b online but i don't understand it at all like why is y = 2r?

Solution for part b:
http://panda.unm.edu/Courses/Price/Phys160/p17-1.pdf

mgL = 1/2mv^2 + mgy

does that formula equals E = KE + PE? So at the highest point the total energy is always KE + PE? Also why is y = 2r?

Help please this is really bothering me! Thanks! :)

 

[CWatters]

I found the solution for part b online but i don't understand it at all like why is y = 2r?

Consider the situation without a peg... The ball would swing back upto the horizontal position. Since that is higher than 2r above the bottom it's clear that when the peg is there the ball will have enough energy to go back up at least 2r.

It can't go any higher than 2r because the string and peg limit it. (I'm ignoring the little bit of string wound around the peg).

 

[CWatters]

Had the ball been dropped from a lower position the problem would have been more difficult. Particularly had it been dropped from a height between r and 2r above the bottom.

If dropped from less than r the tension in the string would remain positive. The ball would swing up, slow, stop and swing down again. At it's highest point KE=0.

If it dropped from a height of between r and 2r it would go up past the peg and tension in the string would be lost. The ball could describe a path similar to this..

 

[CWatters]

does that formula equals E = KE + PE?

Sorry I missed that bit of your question. Yes. Due to conservation of energy the total energy at the top (PE + KE) equals the energy it had at the at the bottom (E).

 

[nchin]

so we are considering the potential energy of the ball with no peg to be 2r? I am sorry i still don't get it. so without the peg, is it like this? so 2r would just be a rough estimate right?

 

[CWatters]

so we are considering the potential energy of the ball with no peg to be 2r?

No. It's at least 2r for the following reason...

1) At the start the PE is mgL.

2) When released the ball swings down and converts that PE into KE = mgL.

3) By inspection of the drawing L > 2r so the KE > mg2r

4) So at the bottom the ball has at least enough KE to swing back up to 2r.

5) It can't swing up more than 2r because the length of the string is fixed. See diagram.

If you still can't follow that let me know which line you get stuck at.

 

[nchin]

No. It's at least 2r for the following reason...

1) At the start the PE is mgL.

2) When released the ball swings down and converts that PE into KE = mgL.

3) By inspection of the drawing L > 2r so the KE > mg2r

4) So at the bottom the ball has at least enough KE to swing back up to 2r.

5) It can't swing up more than 2r because the length of the string is fixed. See diagram.

If you still can't follow that let me know which line you get stuck at.

oooh i see. thanks so much!