Tassandro
- 1
- 0
- Homework Statement
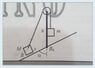
- Two material points of masses M and m are joined together by means of a wire that passes in A through a fixed pulley. The mass m hangs vertically; the largest M rests on a smooth inclined plane that forms an [itex]\alpha[/itex] angle with the vertical. M starts its movement, sliding along the plane, without initial speed, starting from point B0 located on the vertical of A. Demonstrate that point M performs amplitude oscillations [itex] x = \overline {B_oB} = \frac {2m (M-m) h \cos \alpha} {m ^ 2-M ^ 2\cos ^ 2 \alpha} [/itex] where [itex]h = \overline {B_oA} [/itex] and fulfilling the condition [itex] M \cos \alpha < m < M [/itex]
- Relevant Equations
- Gravitational energy: [itex]mgh[/itex]
Last edited by a moderator: