- #1
ExpoDecay
- 6
- 0
Conservation of Energy- A Skier on a Snowball
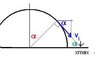
A skier of mass "m" starts at the top of a very large frictionless hemispherical snowball of radius "r" with a very small initial speed and skis straight down the side. Treat the skier as a point particle.
a) At what angle with the vertical does he lose contact with the surface?
b) After flying through the air, the skier hits the ground level with the center of the circular arc. Determine the horizontal distance from the center of the circle to the point of impact on the ground.
Given[r,m]
For part a
Vi=0 Initial Velocity
Y1=r Initial Y
Y2=rcos[itex]\alpha[/itex] Final Y
a(rad)=(v^2)/r Radial Acceleration
n[itex]\rightarrow[/itex]0 The skier loses contact when n goes to zero
K1+U1=K2+U2
For part b
X = xi + ViT + (a(T^2))/2
Part a
I think that I have the correct angle. From the sum of the forces in the y direction, Vf^2=rgcos[itex]\alpha[/itex]
Pluging that into conservation of energy...
mgr=(mVf^2)/2+mgrcos[itex]\alpha[/itex]
cos[itex]\alpha[/itex]=2/3
Part b is where I fall apart.
I know that at the point that the skier loses contact with the snowball, he can be treated as a projectile. And that if I can find the time it takes for the object to move from y1 to y2, I can use it to solve for the horiaontal distance. But I am confused with the initial x and y positions, and the initial velocities in the x and y direction.
Homework Statement
A skier of mass "m" starts at the top of a very large frictionless hemispherical snowball of radius "r" with a very small initial speed and skis straight down the side. Treat the skier as a point particle.
a) At what angle with the vertical does he lose contact with the surface?
b) After flying through the air, the skier hits the ground level with the center of the circular arc. Determine the horizontal distance from the center of the circle to the point of impact on the ground.
Homework Equations
Given[r,m]
For part a
Vi=0 Initial Velocity
Y1=r Initial Y
Y2=rcos[itex]\alpha[/itex] Final Y
a(rad)=(v^2)/r Radial Acceleration
n[itex]\rightarrow[/itex]0 The skier loses contact when n goes to zero
K1+U1=K2+U2
For part b
X = xi + ViT + (a(T^2))/2
The Attempt at a Solution
Part a
I think that I have the correct angle. From the sum of the forces in the y direction, Vf^2=rgcos[itex]\alpha[/itex]
Pluging that into conservation of energy...
mgr=(mVf^2)/2+mgrcos[itex]\alpha[/itex]
cos[itex]\alpha[/itex]=2/3
Part b is where I fall apart.
I know that at the point that the skier loses contact with the snowball, he can be treated as a projectile. And that if I can find the time it takes for the object to move from y1 to y2, I can use it to solve for the horiaontal distance. But I am confused with the initial x and y positions, and the initial velocities in the x and y direction.
Attachments
Last edited: