Conservation of Energy Question

[SoulEater]

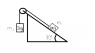
Homework Statement

In the absence of friction, how fast will the masses move after the 2kg mass has dropped 25 cm? [answer: v = 1.57 m/s]

Homework Equations

Conservation of Energy

The Attempt at a Solution

KE2F + KE1F = PE2I + PE1I

.5*m2*vf2^2 + .5*m1*vf1^2 = m2*g*h2 + m1*g*h1

.5 *2*vf2^2 + .5*1*vf1^2 = 2*9.8*.25 + 1*9.8*?

vf2 = vf1

3/2*vf^2 = ?

 

[kuruman]

Hi Souleater, welcome to PF. Conservation of energy is the right approach, but

KE2F + KE1F = PE2I + PE1I

is not correct. The correct form is
KE_I+PE_I=KE_F+PE_F.

 

[SoulEater]

But shouldn't I combine the total energy from both masses?

 

[kuruman]

Yes, and you should also combine the total potential energy for both masses.

Mechanical energy conservation says that

Kinetic plus potential energy of the system at point A is the same as kinetic plus potential energy at point B.

When a mass moves from point A to point B it trades one form of energy for the other form in such a way as to keep the sum the same at all times.

It's like taking money out of your left pocket and putting it in your right pocket. As you do this, you have varying amounts of money in each pocket, but the sum on your person does not change.

 

[SoulEater]

But initially, isn't it all potential energy? Therefore the initial kinetic energy for both masses would be 0.
And at the end of the movement, wouldn't both of the masses have converted that potential energy to kinetic energy? Therefore the potential energy at the end would be 0.

 

[PherricOxide]

The 1kg block will be gaining gravitational potential energy as it rises.

 

[tiny-tim]

Welcome to PF!

Hi SoulEater! Welcome to PF!

KE + PE = constant. ​

 

[SoulEater]

Thank you.

So how would the equation look like?

 

[tiny-tim]

ke1f + ke2f + pe1f + pe2f = ke1i + ke2i + pe1i + pe2i