unscientific
- 1,728
- 13
Homework Statement
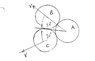
The problem is given in the picture: (please refer to the 2 pictures below, thank you!)
I'm having trouble with the last part...
Homework Equations
Conservation of momentum in both x and y - directions.
The Attempt at a Solution
From symmetry it can be seen that ball D would be directly below ball C, with ball C moving at speed of (2/5)sqrt(3)*u at an angle of 30 degrees below horizontal.
Here's my attempt using the x-y direction conservation of momentum
Taking downwards and leftwards as positive,
Horizontally:
There would be no transfer in horizontal momentum to ball D, hence ball C still would have a horizontal velocity of: (3/5)u
Vertically (downwards as positive):
sqrt(3)/5 * u = vc cosθ + vD
Energy equation:
(12/25)u2 = (vc)2 + (vD)2
That leaves me with 2 equations with 3 unknowns, vc, vD and θ.
I tried using a new approach, but would like to ask if this obeys the laws of physics:
Horizontal speed of c: unchanged = (3/5)u
Considering collision "vertically":
can i simply do the momentum equation by solely considering only the vertical velocities?
(1/5)sqrt(3)* u = Vc,y + VD
Again only considering energy in the vertical direction: ( i know this is wrong as energy is not a vector!):
(9/25)u2 = (vc,y)2 + (vD )2
This allows me to solve the problem, but is this the right approach?
Here's a quick, not-so-rigorous proof: vx2 + vy2 = v'2, multiplying (1/2)m throughout... gives us the split energy equation!)
Attachments
Last edited: