Constraint of Two blocks on an inclined plane

[CGandC]

Hello,

I have an issue regarding a constraint related to an angle:

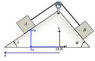
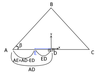
Suppose I have masses 'A' and 'B' on an inclined plane ( of mass 'C') attached by a pulley.

I place my origin as shown and I want to find a constraint relating angle β.

so, I saw my classmate writing as follows to find that constraint:

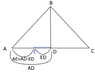
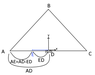
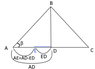
tan(β) = (Ya)/(P-Xa)

So my questions are:
1. why I can't define the constraint as tan(β) = (Ya)/(Xa-P) rather then tan(β) = (Ya)/(P-Xa)
2. what does the expression 'P-Xa' mean? it can't be length because it is negative, so I thought - is it the displacement of the wedge relative to mass A? but what about the angle β being negative? ( it is supposed to be positive)

Notes:
- 'Xa' and 'Ya' are the coordinates of mass 'A'
- 'P' is the coordinate of the leftmost vertice of the triangle
-The coordinates need to stay as they are, this is part of what makes up the difficulty.

 

[FilipLand]

You could do that.
It all depends on how you define the directions of the axes, which you are always free to do however you want unless the exercise states otherwise, which it has done in this case.

p-x is not equal to x-p, but abs.(p-xa) ia always equal to abs.(xa-p). Length is always a absolute value, but we are sloppy and not always write it out since it is very often already positive.

And P is always greater then xa so you for that reason you take P-xa, but, if you like you could take the absolutvalue of xa-P, i.e. tan(B) = (Ya)/(abs.(xa-p))

 

[haruspex]

P is always greater then xa

Is that what you meant? As I read the question, those are both negative and P has the greater magnitude, so P<Xa.

 

[CGandC]

You could do that.
It all depends on how you define the directions of the axes, which you are always free to do however you want unless the exercise states otherwise, which it has done in this case.

p-x is not equal to x-p, but abs.(p-xa) ia always equal to abs.(xa-p). Length is always a absolute value, but we are sloppy and not always write it out since it is very often already positive.

And P is always greater then xa so you for that reason you take P-xa, but, if you like you could take the absolutvalue of xa-P, i.e. tan(B) = (Ya)/(abs.(xa-p))

Is that what you meant? As I read the question, those are both negative and P has the greater magnitude, so P<Xa.

according to my coordinates ( which I cannot change) P<Xa

 

[FilipLand]

according to my coordinates ( which I cannot change) P<Xa

How is the purple arrow smaller then the blue one "xa" in the figure?

 

[haruspex]

How is the purple arrow smaller then the blue one "xa" in the figure?

It is a longer arrow, but that only means it has greater magnitude. E.g. -2 > -3.

 

[CGandC]

I think I should write the constraint as : ' tan(β) = (Ya)/(Xa-P) ' and that is because ' Xa-P > 0 ' if this assumption is correct, then why would anyone want to write 'tan(β) = (Ya)/(P-Xa)' where 'P-Xa < 0' ?

 

[haruspex]

write the constraint as : ' tan(β) = (Ya)/(Xa-P) '

Yes.

why would anyone want to write 'tan(β) = (Ya)/(P-Xa)' where 'P-Xa < 0' ?

Because they are confused over displacement versus distance. Or you could define β as the angle to the leftward segment of the x axis.

 

[CGandC]

Yes.

Because they are confused over displacement versus distance. Or you could define β as the angle to the leftward segment of the x axis.

I understand your reasoning, but my classmate looked at the problem in a geometrical way which perplexed me :

Let's say geometrically , if I have a triangle as shown below , and I want to calculate 'AE' then I work it out as:
' AE = AD-ED '

now, If I want to put the same triangle in a coordinate system as shown below then a fortiori , 'AE' should still be
calculated the same way , as shown below

( 'AE = AD - ED' , where AD<ED<0 because of the coordinates )

using this line of reasoning, I deduce that the constraint should be written as:
tan(β) = (Ya)/(P-Xa) ( where P-XA is just like AD-ED )
and not: tan(β) = (Ya)/(Xa-P)

So does this make what we agreed on - that the constraint is 'tan(β) = (Ya)/(Xa-P) ' as false?

 

[haruspex]

So does this make what we agreed on - that the constraint is 'tan(β) = (Ya)/(Xa-P) ' as false?

As I wrote, it all depends whether you are treating P and Xa as displacements or distances.

The geometrical argument makes them distances. Distances are unsigned scalars, so non-negative. Consequently, in that view, P>Xa and P-Xa is positive.

In your own approach, P and Xa are displacements from the origin, in the negative direction. Displacements are vectors, so signed. In this view, Xa>P.

Both approaches are valid and produce the right result. Arguably, the vector approach is more general. In some contexts, you do not know in advance which distance is the greater. Vectors handle that uncertainty better than scalars do.

 

[CGandC]

As I wrote, it all depends whether you are treating P and Xa as displacements or distances.

The geometrical argument makes them distances. Distances are unsigned scalars, so non-negative. Consequently, in that view, P>Xa and P-Xa is positive.

In your own approach, P and Xa are displacements from the origin, in the negative direction. Displacements are vectors, so signed. In this view, Xa>P.

Both approaches are valid and produce the right result. Arguably, the vector approach is more general. In some contexts, you do not know in advance which distance is the greater. Vectors handle that uncertainty better than scalars do.

So from what I understand , solving a physics problem has two approaches:
1. geometrical approach( distances only, there is no negative distance and no vectors)
2. analytical geometry approach ( there's coordinate axis and we can have here distances , displacements, vectors... )

What I did in this problem is to approach it using techniques of analytical geometry rather then pure geometry and not knowing the difference between the two approaches entirely ... that is why I was having difficulty about wether in the constraint there should be 'Xa-P' or 'P-Xa' , Do you agree?

 

[haruspex]

So from what I understand , solving a physics problem has two approaches:
1. geometrical approach( distances only, there is no negative distance and no vectors)
2. analytical geometry approach ( there's coordinate axis and we can have here distances , displacements, vectors... )

What I did in this problem is to approach it using techniques of analytical geometry rather then pure geometry and not knowing the difference between the two approaches entirely ... that is why I was having difficulty about wether in the constraint there should be 'Xa-P' or 'P-Xa' , Do you agree?

Yes.