SUMMARY
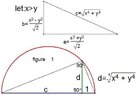
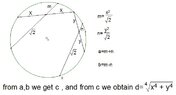
The discussion focuses on constructing a segment of length $\sqrt[4]{x^4+y^4}$ using a straightedge and compass, based on two given segments of lengths $x$ and $y$. Participants debated the validity of solutions that involve using a calculator versus purely geometric constructions. A key point raised is the convention that straightedges are unmarked, which complicates the use of segments like $1$ and $\sqrt{2}$ in the construction. Ultimately, the geometric construction proposed by one participant is deemed valid, while reliance on calculated values is contested.
PREREQUISITES
- Understanding of straightedge and compass constructions
- Familiarity with geometric principles and conventions
- Knowledge of segment lengths and their relationships
- Basic algebra involving roots and powers
NEXT STEPS
- Research geometric constructions involving square roots and higher roots
- Explore the implications of using unmarked straightedges in constructions
- Study methods for constructing segments from given lengths using straightedge and compass
- Investigate the relationship between segment lengths and their geometric representations
USEFUL FOR
Mathematicians, geometry enthusiasts, educators teaching geometric constructions, and students studying classical construction methods.