Constructing an op amp circuit of variable gain neg to pos

[mathg33k]

Homework Statement

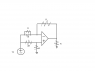
Suppose you are given an ideal op amp, an ideal voltage source with voltage Vs, 5 resistors with resistance R, and one variable resistor whose resistance can be adjusts continuously between .2R and R. Use these components to design a circuit, assuming ideal op-amp behavior, that provides an output voltage Vo given by Vo = GVo, where G can be adjusted continuously from -.5 to +.5 by adjusting the resistance of the variable resistor over its full range of values. Note that the voltage source can be connected to multiple points in the circuit

Homework Equations

V- = V+
I- = I+ = 0

The Attempt at a Solution

Based on the output voltage GVo I assume the op amp would take the model of an inverting amp, with resistors Rs and Rf. Therefore it would theoretically follow the node equation
(Vn - Vs) / (xR) + (Vn - Vo) / (aR) = 0, where xR would be a value of resistor I could create from the extra resistors I have. From here I simplify to (1/(aR) + 1/(xR)) Vn + (-1/(xR))Vs = Vo /(aR). I'm very confused though, because it seems impossible to use a pot/var resistor for negative output if it does not go to 0. I don't understand how using all positive resistors one would be able to invert output when you go across its range.

Because resistance is inversely related to voltage, across the range .2 to 1 I would get coefficients of 1 and 5 in the equation but I don't know how to shift this range 1-5 to -.5 to .5 (shrinking the range is easy but subtracting a constant value, constricted to the materials given? )

 

[aralbrec]

Because resistance is inversely related to voltage, across the range .2 to 1 I would get coefficients of 1 and 5 in the equation but I don't know how to shift this range 1-5 to -.5 to .5 (shrinking the range is easy but subtracting a constant value, constricted to the materials given? )

You can add an offset by attaching a voltage source to the + terminal of the inverting configuration. Superposition will have the source on the + terminal add a fixed voltage to the output. The voltage source can then be replaced by a voltage divider from the supply since the + terminal draws no current. However, because your gain is variable, the offset will also be variable so this is not good here.

There is another way to get positive and negative values and that is through subtraction (difference amplifier). That, with the hint given, maybe can steer you in a fruitful direction.

 

[mathg33k]

Hello aralbrec, thanks for your hint! I was able to solve the problem by connecting Vs to the negative input in series with two parallel resistors R, and connecting Vs to the positive input with variable resistor aR and one resistor R leading to ground. Then the other two R were used for the feedback loop and load resistor out of Vo.
However I only found the solution through trial and error and I feel that solving this problem repeatedly with different values would be troublesome!

Thanks again.

 

[aralbrec]

However I only found the solution through trial and error and I feel that solving this problem repeatedly with different values would be troublesome!

Did you also manage to deal with a being in range 0.2 to 1 instead of 0 to 1?

I can tell you I have spent much too much time on this as well -- close to an hour but I'll tell you how I finally worked it out.

I started with the general difference amp (see diagram "difference.png") on the left. I wrote out the transfer function which you can find with superposition (set Vi to 0 at + terminal, then Vi to 0 on - terminal).

$\frac{Vo}{Vi}=-\frac{R2}{R1}+(\frac{R4}{R3+R4})(1+\frac{R2}{R1}) =\frac{R1R4 - R2R3}{R1R4 + R1R3} =\frac{1 - \frac{R2}{R1}\frac{R3}{R4}}{1 + \frac{R3}{R4}}$

In the last step I divided by R1R4 because it is the ratio of resistors that are important since all will be some sort of multiple of R.

We want the gain to be between -0.5 and +0.5:

$-0.5≤\frac{1 - \frac{R2}{R1}\frac{R3}{R4}}{1 + \frac{R3}{R4}}≤0.5$

By setting R3=R4=R I get a 2 on the bottom which changes the inequality to:

$-1≤1 - \frac{R2}{R1}≤1$

If R2/R1 is 0, I get 1, the right side of the inequality
If R2/R1 is 2, I get -1, the left side of the inequality.

This will work if R2 is the variable resistor aR, 0≤a≤1 and R1=R/2

This circuit is drawn on the right side of the attached difference.png and the overall transfer function is:

$\frac{Vo}{Vi}=\frac{1-2a}{2}$

If a=0, Vo/Vi = 0.5
If a=1, Vo/Vi = -0.5

Just as desired except for one problem -- a can only go as low as 0.2. I tried fiddling around with that for a bit and found a new approach instead.

============

I started by building in the limitation of the variable resistor into the equations. The variable resistor ranges from 0.2R to R so I modeled that as a resistance 0.2R + 0.8aR where a can again range from 0 to 1.

I started with the simple voltage divider with R in series with the variable resistor as shown in diagram "secondapproach.png". The transfer function is:

$\frac{Vb}{Vi}=\frac{0.2R+0.8aR}{R+0.2R+0.8aR}= \frac { 1+4a}{6+4a}$

So Vb goes from Vi/6 (a=0) to Vi/2 (a=1), a range of 1/2-1/6 = Vi/3

The target range is -0.5 to 0.5 times Vi, a range of 0.5--0.5 = 1. So the next step was to multiply the above by 3 to get the range of 1. I chose to hook it up the voltage divider to a non-inverting op amp with gain 3. The reason was to keep Vb separate from the gain circuit. In the non-inverting configuation, the gain is (1+R2/R1) so for a total gain of 3, I want R2/R1 = 2 which is possible if R2=R and R1=R/2. The result is the second diagram in "secondapproach.png". The transfer function is now:

$\frac{Vo}{Vi} = \frac{Vb}{Vi}(1+\frac{R}{R/2})=3\frac{Vb}{Vi}= \frac{3+12a}{6+4a}$

The output range is now 0.5Vi (a=0) to 1.5Vi (a=1), a range of 1.5-0.5=1Vi just like we wanted.

Next step is to notice that if Vi is subtracted from Vo, the output will range from -0.5Vi (a=0) to 0.5Vi (a=1), which is exactly what is wanted. The idea was to use an inverting configuration to add -Vi to the output. So I grabbed one of the parallel R and attached it to Vi to get the final circuit in the attached diagram.

The idea was that Vb is not affected by doing this so its voltage appears fixed at the negative terminal of the opamp. This means I can treat that voltage at the -ve terminal as a voltage source and the total Vo can be found by superposition with the voltage at the -ve terminal first at Vb with Vi set to zero (but only the Vi going through the parallel resistor!) which gets the transfer function we already have. Then the voltage at the -ve terminal is set to 0 with Vi attached to the parallel resistor. The current from Vi flows to the virtual ground and *all* of it goes through the feedback resistor to get a gain of -R/R=-1. The other parallel resistor still connected to ground is shorted out by the virtual ground and does not do anything.

The final transfer function I found by writing KCL at the negative terminal where the voltage there is Vb. I did it this way to make sure my thinking was right.

$\frac{Vo}{Vi}=\frac{8a-3}{6+4a}$

The output is now -0.5 Vi for a=0 and 0.5 Vi for a=1.

This seems to be more suited to a take home problem than an exam problem unless someone can think of a simpler way to do this.

 

[mathg33k]

This was actually an exam problem on last year's final at University of Texas worth ~15 pts. The teacher I have is notorious for his classes' difficulty. The averages on these tests are in the 40s.. but they are curved.
Attached is a diagram of my solution.

(Vn - Vs)/(R/2) + (Vn - Vo)/R = 0
(Vp - Vs)/(.2R) + Vp/R = 0
From equation 2, Vp = Vn = (5/6) Vs
From equation 1, Vo = 3Vn - 2Vs -> (3*5/6 - 2) Vs = .5Vs

(Vn - Vs)/(R/2) + (Vn - Vo)/R = 0
(Vp - Vs)/(R) + Vp/R = 0
From equation 2, Vp = Vn = Vs/2
From equation 1, Vo = 3Vn - 2Vs -> (3*1/2 - 2) Vs = -.5Vs