Callum Plunkett
- 27
- 8
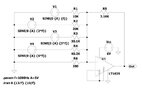
I did that in an earlier attempt at the question, I can't remember why now but I decided to ty a different method. Might have to reconsider going back to it.Baluncore said:Did you consider simply adding a DC current to the AC harmonic currents at the summing input?
That way it provides the offset without needing a second op-amp.