Pruddy
- 64
- 0
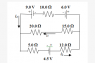
1) Please take a look at the attachment below in order to solve the problem. Using the figure at the right determine the values of i1, i2 and i3. Input your answers in the form "a.bc x 10^(y) A".
2) Using the correct results from #1, determine the following. For A and B you must also tell if the current directions shown are correct. Give your answer in the requested format.
A. The current in the 10.0 resistor. Answer format: "abc mA, Y/N" . Y/N means choose Y if the current is as shown, and choose N if the direction of the current is not correct.
B. The current in the 4.5 V battery. Answer format: "abc mA, Y/N" . Y/N means choose Y if the current is as shown, and choose N if the direction of the current is not correct.
C. The voltage across the 15.0 resistor. Answer format: "ab.c V".
D. How much power is dissipated in the 5.0 resistor? Answer Format: "abc mW"
I was able to solve i2, i1, and i3 from the loop equation
Loop: i1(10Ω) - 9.0V + 6.0 V - i3(15Ω+20Ω) = 0
Loop: i3(15Ω+20Ω)+i2(5Ω+12Ω) - 4.5V = 0
Loop: i1(10Ω) - 9.0V + 6.0V + i2(12Ω + 5Ω) - 4.5V = 0
Junction: i1 + i3 = i2
i3 = -6/170 A ≈ -0.005381 A
i1 = ( -0.005381(15Ω+20Ω) + 3)/10 = 0.2811665
i2 = (4.5 - (-0.005381 (15Ω+20Ω))/(5Ω+12Ω)) = 0.2757844
The next problem that we should find the current in the 10.0Ω resistor and the current in the 4.5 V battery. And also to state if the direction of the current is correct or not using the loop equations
I believe the current in the 10Ω resistor is i1 = 0.2811665 and the current in the 4.5 V is equal to
0.2757844 and the directions of the current is correct according to the loop equations. I am not to sure if my answers are correct or not. I will be very grateful if anyone can help.
I have two more other questions.
Please i) how do i calculate the voltage across the 15.0 resistor
ii) How much power is dissipated in the 5.0 resistor
2) Using the correct results from #1, determine the following. For A and B you must also tell if the current directions shown are correct. Give your answer in the requested format.
A. The current in the 10.0 resistor. Answer format: "abc mA, Y/N" . Y/N means choose Y if the current is as shown, and choose N if the direction of the current is not correct.
B. The current in the 4.5 V battery. Answer format: "abc mA, Y/N" . Y/N means choose Y if the current is as shown, and choose N if the direction of the current is not correct.
C. The voltage across the 15.0 resistor. Answer format: "ab.c V".
D. How much power is dissipated in the 5.0 resistor? Answer Format: "abc mW"
I was able to solve i2, i1, and i3 from the loop equation
Loop: i1(10Ω) - 9.0V + 6.0 V - i3(15Ω+20Ω) = 0
Loop: i3(15Ω+20Ω)+i2(5Ω+12Ω) - 4.5V = 0
Loop: i1(10Ω) - 9.0V + 6.0V + i2(12Ω + 5Ω) - 4.5V = 0
Junction: i1 + i3 = i2
i3 = -6/170 A ≈ -0.005381 A
i1 = ( -0.005381(15Ω+20Ω) + 3)/10 = 0.2811665
i2 = (4.5 - (-0.005381 (15Ω+20Ω))/(5Ω+12Ω)) = 0.2757844
The next problem that we should find the current in the 10.0Ω resistor and the current in the 4.5 V battery. And also to state if the direction of the current is correct or not using the loop equations
I believe the current in the 10Ω resistor is i1 = 0.2811665 and the current in the 4.5 V is equal to
0.2757844 and the directions of the current is correct according to the loop equations. I am not to sure if my answers are correct or not. I will be very grateful if anyone can help.
I have two more other questions.
Please i) how do i calculate the voltage across the 15.0 resistor
ii) How much power is dissipated in the 5.0 resistor
Attachments
Last edited: