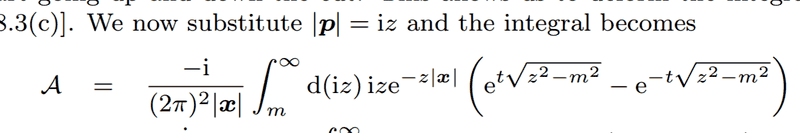SUMMARY
The forum discussion centers on understanding the transformation of integrals in quantum field theory, specifically from the book "QFT for the Gifted Amateur." The integral in question is manipulated from the limits of integration from \(-\infty\) to \(0\) and \(0\) to \(\infty\) to a form that includes a substitution of \(|p| = iz\). The participants clarify that changing the limits of integration introduces a negative sign, yet the substitution of \(-|p|\) maintains the integrity of the integral. This highlights the importance of careful manipulation of limits and substitutions in complex integrals.
PREREQUISITES
- Understanding of complex analysis and contour integration
- Familiarity with quantum field theory concepts
- Knowledge of integral calculus and properties of definite integrals
- Experience with exponential functions and their properties in integrals
NEXT STEPS
- Study the application of Jordan's lemma in contour integration
- Learn about the Cauchy integral theorem and its implications in quantum field theory
- Explore the substitution techniques in complex integrals, particularly in quantum mechanics
- Review the properties of Fourier transforms in relation to quantum field theory
USEFUL FOR
This discussion is beneficial for physicists, mathematicians, and students engaged in quantum field theory, particularly those looking to deepen their understanding of integral transformations and complex analysis techniques.
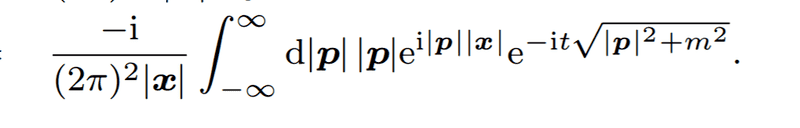 becomes
becomes