- #1
hypernihl
- 8
- 0
Coordinate System of Coupled Oscillators and "4D" Phase Space representation
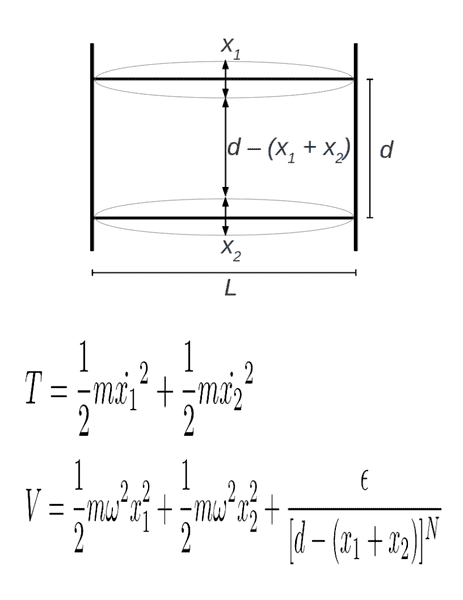
So, I've modeled the interaction between two cantilever beams with the kinetic and potential energies shown in the above figure. The cantilevers are very stiff and have a small oscillation amplitude, so they can be modeled as two interacting springs. In the coupling potential epsilon and N > 0.
I'm having a little trouble wrapping my head around the "signs (+ or -)" in the equations of motion derived from the Lagrangian.
Have I set this up right?
All so, I have been displaying the phase-space by potting v1+v2 vs d-(x1+x2).
I'd appreciate any thoughts on this.
Thanks
So, I've modeled the interaction between two cantilever beams with the kinetic and potential energies shown in the above figure. The cantilevers are very stiff and have a small oscillation amplitude, so they can be modeled as two interacting springs. In the coupling potential epsilon and N > 0.
I'm having a little trouble wrapping my head around the "signs (+ or -)" in the equations of motion derived from the Lagrangian.
Have I set this up right?
All so, I have been displaying the phase-space by potting v1+v2 vs d-(x1+x2).
I'd appreciate any thoughts on this.
Thanks