Could someone me to read the following line

[EnglsihLearner]

Could someone please help me to read the following line(in case of inner product)?

 

[jbunniii]

The statement indicates that $\langle \cdot, \cdot \rangle$ is a map from $V \times V$ to $F$. This means that to each ordered pair $(u,v)$ with $u,v \in V$, it assigns an element $\langle u,v \rangle$ in $F$.

Presumably $F$ is a field, and $V$ is a vector space over $F$.

 

[EnglsihLearner]

The statement indicates that $\langle \cdot, \cdot \rangle$ is a map from $V \times V$ to $F$.

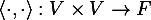
Yes, I understand now. Could you please explain what does "map" mean here?As I know map means the following-

https://www.google.com.bd/search?bi....0..0.0...0...1c.1.24.serp..3.0.0.hrQDtAr7Tpw

If it is same here then I would request you to explain again the following part-

that $\langle \cdot, \cdot \rangle$ is a map from $V \times V$ to $F$

 

[jbunniii]

Yes, I understand now. Could you please explain what does "map" mean here?

In mathematics, "map" and "function" mean the same thing.