- #1
Math Amateur
Gold Member
MHB
- 3,990
- 48
I am reading the book: Multivariable Mathematics by Theodore Shifrin ... and am focused on Chapter 8, Section 2, Differential Forms ...
I need some help in order to fully understand the vector space of alternating multilinear functions ...
The relevant text from Shifrin reads as follows:

In the above text from Shifrin we read the following:
" ... ... In particular, if ##T \in {\bigwedge}^k ( \mathbb{R}^n )^{ \ast }##, then for any increasing ##k##-tuple ##I##, set ##a_I = T( e_{ i_1} , \cdot \cdot \cdot , e_{ i_k} )##. Then we leave it to the reader to check that##T = \sum_{ i \text{ increasing } }a_I \text{dx}_I##
... ... ... "
Can someone please help me to prove/demonstrate that ##T = \sum_{ i \text{ increasing } }a_I \text{dx}_I## ... ...
Help will be much appreciated ...
Peter
==========================================================================================In case someone needs access to the text where Shifrin defines the terms of the above post and explains the notation, I am providing access to the start of Chapter 8, Section 2.1 as follows:

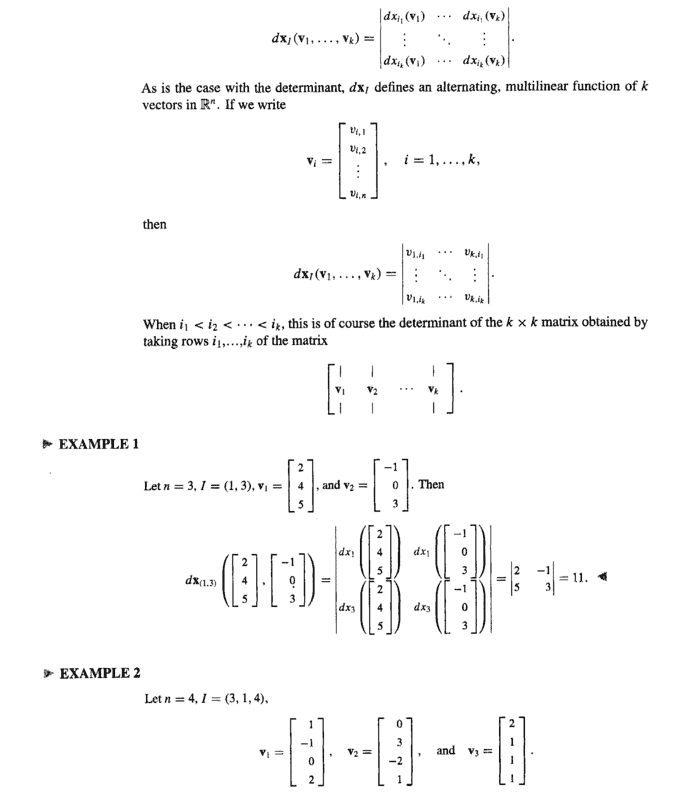

Hope that helps ...
Peter
I need some help in order to fully understand the vector space of alternating multilinear functions ...
The relevant text from Shifrin reads as follows:
In the above text from Shifrin we read the following:
" ... ... In particular, if ##T \in {\bigwedge}^k ( \mathbb{R}^n )^{ \ast }##, then for any increasing ##k##-tuple ##I##, set ##a_I = T( e_{ i_1} , \cdot \cdot \cdot , e_{ i_k} )##. Then we leave it to the reader to check that##T = \sum_{ i \text{ increasing } }a_I \text{dx}_I##
... ... ... "
Can someone please help me to prove/demonstrate that ##T = \sum_{ i \text{ increasing } }a_I \text{dx}_I## ... ...
Help will be much appreciated ...
Peter
==========================================================================================In case someone needs access to the text where Shifrin defines the terms of the above post and explains the notation, I am providing access to the start of Chapter 8, Section 2.1 as follows:
Hope that helps ...
Peter
Attachments
-
 Shifrin - Alternating Multilinear Functions ... .png71.6 KB · Views: 456
Shifrin - Alternating Multilinear Functions ... .png71.6 KB · Views: 456 -
 ?temp_hash=c5a985b43e67ff351bbb3452d56f5618.png71.6 KB · Views: 870
?temp_hash=c5a985b43e67ff351bbb3452d56f5618.png71.6 KB · Views: 870 -
 Shifrin - 1 - Start of Ch. 8, Section 2.1 ... Differential Forms ... PART 1 ... .png47.6 KB · Views: 261
Shifrin - 1 - Start of Ch. 8, Section 2.1 ... Differential Forms ... PART 1 ... .png47.6 KB · Views: 261 -
 Shifrin - 2 - Start of Ch. 8, Section 2.1 ... Differential Forms ... PART 2 ... .png18.8 KB · Views: 317
Shifrin - 2 - Start of Ch. 8, Section 2.1 ... Differential Forms ... PART 2 ... .png18.8 KB · Views: 317 -
 Shifrin - 3 - Start of Ch. 8, Section 2.1 ... Differential Forms ... PART 3 ... .png48.5 KB · Views: 253
Shifrin - 3 - Start of Ch. 8, Section 2.1 ... Differential Forms ... PART 3 ... .png48.5 KB · Views: 253 -
 ?temp_hash=a6ac9c21b636d70cd5c23e172af350a3.png47.6 KB · Views: 897
?temp_hash=a6ac9c21b636d70cd5c23e172af350a3.png47.6 KB · Views: 897 -
 ?temp_hash=a6ac9c21b636d70cd5c23e172af350a3.png18.8 KB · Views: 899
?temp_hash=a6ac9c21b636d70cd5c23e172af350a3.png18.8 KB · Views: 899 -
 ?temp_hash=a6ac9c21b636d70cd5c23e172af350a3.png48.5 KB · Views: 799
?temp_hash=a6ac9c21b636d70cd5c23e172af350a3.png48.5 KB · Views: 799
Last edited: