BobRoss
- 34
- 0
I'm having a bunch of trouble with an electrostatics questions as well as an electric fields question. I'll start with the electrostatics problem.
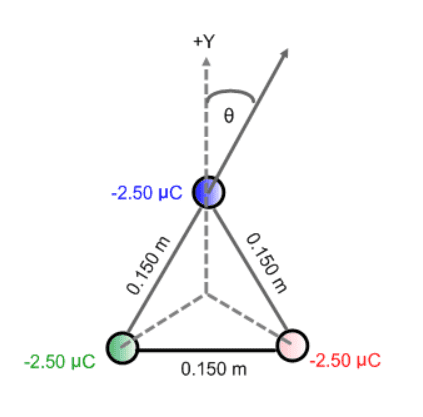
I am given the following equilateral triangle and asked to calculate the net electrostatic force on each charge.
Fe=[kq1q2]/r2
So since the charges are all equal and the distances between them are all equal, the force of the blue on red is equal to the force of red on green which is equal to the green on the blue. So I find:
Fe=[kq1q2]/r2
Fe=[(8.99x109)(2.50x10-6C)(2.50x10-6C)]/(0.150 m)2
Fe=2.4972 N/C
I don't really know how to proceed past this. I think I need to break things down into x and y components but I don't know how I would draw those here. I know that since all of the charges are negative they will be repelling each other but how do I figure out the magnitude and direction of that repulsion?
Homework Statement
I am given the following equilateral triangle and asked to calculate the net electrostatic force on each charge.
Homework Equations
Fe=[kq1q2]/r2
The Attempt at a Solution
So since the charges are all equal and the distances between them are all equal, the force of the blue on red is equal to the force of red on green which is equal to the green on the blue. So I find:
Fe=[kq1q2]/r2
Fe=[(8.99x109)(2.50x10-6C)(2.50x10-6C)]/(0.150 m)2
Fe=2.4972 N/C
I don't really know how to proceed past this. I think I need to break things down into x and y components but I don't know how I would draw those here. I know that since all of the charges are negative they will be repelling each other but how do I figure out the magnitude and direction of that repulsion?