Alistair Vowles
- 2
- 0
I hope this will be an easy one to answer that I could just use a little help with.
I have an L shaped bar where 'X' is on a flat surface. The pivot point is the circle.
Can someone help me with a formula to calculate the force needed at point 'b' , given a certain force applied at point 'a' , to not allow the bar to pivot.
Force 'a' will be a varying force (wind) so I want to make sure I have enough counterweight for force 'b' to allow for this variable.
The fig is not to scale and I plan to have the length of 'X' to be adjustable to decrease the force needed at point 'b' .
I hope this makes sense and thank you for the help !
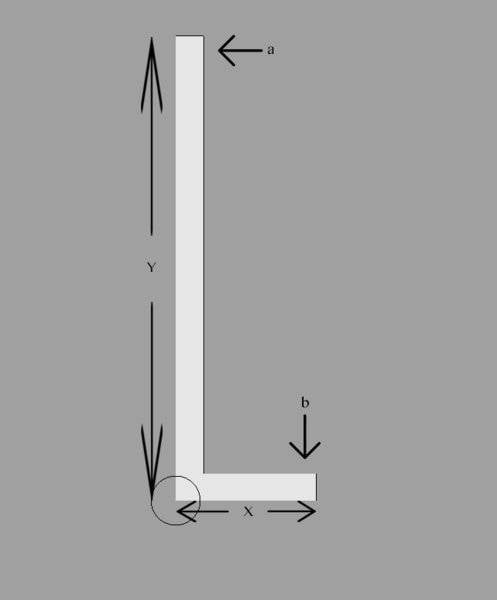
I have an L shaped bar where 'X' is on a flat surface. The pivot point is the circle.
Can someone help me with a formula to calculate the force needed at point 'b' , given a certain force applied at point 'a' , to not allow the bar to pivot.
Force 'a' will be a varying force (wind) so I want to make sure I have enough counterweight for force 'b' to allow for this variable.
The fig is not to scale and I plan to have the length of 'X' to be adjustable to decrease the force needed at point 'b' .
I hope this makes sense and thank you for the help !
