Creating an Ohmmeter: Solving a HW Problem Using Kirchov's Laws

[jnol6056]

Here is the pblm, but i can't seem to get a foothold as where to start. I've tried starting with Kirchov's Laws, but can't see to get anywhere with them. Plz help.


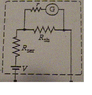
*One type of ohmmeter consists of an ammeter connected to a series resistor and a battery. The scale is different from ammeters and voltmeters. Zero resistance correspodns to full-scale deflection (because maximum current flows from the battery), whereas infinite resistance corresponds to no deflection (no current flow). Suppose a 3.0V battery is used, and a glavanometer that has an internal resistance of 25ohms and deflects full-scale for a current of 35 microAmps. What values of shunt resistance, R(shunt), and series resistance, R(series), are needed to make an ohmmeter that registers a mid-mid scale deflection( that is half the max) for a resistance of 30ohms? [Note: and additional series resistor ( variable) is also needed so the meter can be zeroed. the sero should be checked frequently by touching the leads together, sinc e the battery voltage can vary. Because of battery voltage variation, such ohmmeters are not precision instruments, but they are useful to obtain approx. values.]

 

[jnol6056]

here is what I have so far as to the equations that I'm using:

C: I1-I2-I3=0
Loop 1: 3-I1*R(series)-I3*R(shunt)=0
Loop 2: -I2*r-I2*R(G)+I3*R(shunt)=0

My first question, should I use the 30ohm measured resistance along with I1 in loop 1? And my second question, is the value for I2*r irrelivant to the equation since it is a variable resistance and the voltage being used is a constant of 3V? And if so, would I2=35microamperes?

 

[Chen]

You know that the galvanometer deflects fully for a current of 35uA, so if you want it to deflect halfway you need a current of 17.5uA, let's call it I(r). R(L) will be 30ohm, which is the resistance you measure. If I(sh) is the current through shunt resistance, then I(ser), the current through the battery, is I(sh) + 17.5uA. So you have three uknowns: R(sh), R(ser) and I(sh). That's one uknown too many, since you only have two loops to solve:

3v = R_{ser}(I_{sh} + I_r) + R_L(I_{sh} + I_r) + rI_r
3v = R_{ser}(I_{sh} + I_r) + R_L(I_{sh} + I_r) + R_{sh}I_{sh}

So what we do is express I(sh) as a function R(sh). You know that the potential drop on r and R(sh) is equal, so:

V_r = V_{sh} = rI_r = R_{sh}I_{sh}

Therefore:

I_{sh} = I_r\frac{r}{R_{sh}}

So you now have two uknowns with two equations:

3v = R_{ser}(I_r\frac{r}{R_{sh}} + I_r) + R_L(I_r\frac{r}{R_{sh}} + I_r) + rI_r
3v = R_{ser}(I_r\frac{r}{R_{sh}} + I_r) + R_L(I_r\frac{r}{R_{sh}} + I_r) + R_{sh}I_r\frac{r}{R_{sh}}

Except that the 2nd equation is actually identical to the 1st equation, so you still have one variable too many. I don't really see how you can solve this question, so I'm guessing that they are asking just for any two values that will work.^* If that's the case, you can solve the first equation for R(ser):

R_{ser} = \frac{3v - R_L(I_r\frac{r}{R_{sh}} + I_r) - rI_r}{I_r\frac{r}{R_{sh}} + I_r}

And now you can just pick whatever value you want for R(sh) and get the corresponding value for R(ser). For example, for R(sh) = 50ohm you would get R(ser) = 114.2kohm. Or for R(sh) = 5ohm you would get R(ser) = 28.5kohm. Or for R(sh) = 1ohm you would get R(ser) = 6.6kohm.


^* I might be wrong there, so feel free to correct me anyone.

 

[jnol6056]

What about the constraint equation I1-I2-I3=0? Wouldn't that count as a third equation for figuring out the two resistances? Also, I was wondering if you could include a 30ohm resistor since that is what is being measured.

 

[Chen]

I did include a 30ohm resistor, that's R(L). As for the constraint equation, it wouldn't help in this case. The only current in our final equation is I(r), so even though constraint equation is correct, it's not very useful. This is because I already used it when I said "If I(sh) is the current through shunt resistance, then I(ser), the current through the battery, is I(sh) + 17.5uA."