- #1
tworitdash
- 107
- 26
I am trying to simulate and process the Doppler signals. My main problem is a little more complex so I am only posting a simple version of it. Task1: I have a time-domain signal with the velocity of the target as mu. I need to change the velocity to mu cos(theta) where theta is a vector from 0 to 2 pi with the same number of points that I have in the time domain signal. So, every point in the original time-domain signal should have this change. This means that the Doppler frequency (velocity) is not constant with time. Task2: Then, after I get this signal, I want to recover the original spectrum (with constant velocity) but without knowing mu. I just need to know the phase and then modify it somehow to get the real signal.
The figure is shown below. The Yellow plot should resemble the blue blot but it doesn't. Any idea what I do wrong here? The red plot also should show multiple spikes in the plot and not like a noise signal like this I suppose.
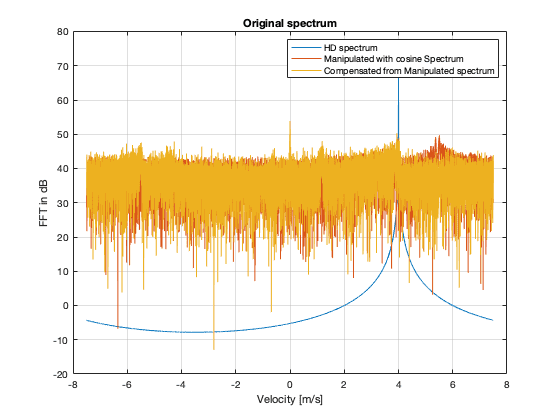
Task1 and Task2:
clear;
close all;
lambda = 0.03;
M = 61;
hs = 128;
N = hs * M; % Number of points in the time axis
mu = 4; % Doppler velocity
PRT = 1e-3; % Time step
t1 = 0:PRT:(N - 1)*PRT; % Time axis
s_ = exp(1j .* 4 * pi ./ lambda .* mu .* t1); % Original Time domain signal
s_f = fftshift(fft(s_)); % FT of the original time domain signal
v_amb = 7.5;
v_axis = linspace(-N/2, N/2-1, N)/N .* 2 * v_amb; % Velocity axis
figure; plot(v_axis, db(abs(s_f))); title('Original spectrum') % Original spectrum
%% Task1:
BW = 1*pi/180;
p0 = 0*pi/180;
p1 = 360*pi/180;
th = linspace(p0, p1, N); % Angle axis for cos(theta)
s_man_ = abs(s_) .* exp(1j .* (angle(s_)) + 1j * 4*pi/lambda * mu * (cos(th) - 1) .* t1); % Modified time domain signal with cos(theta)
s_man_f_full = fftshift(fft(s_man_)); % FT of the modified time domain signal
%% Task 2
s_man_comp = abs(s_man_) .* exp(1j .* (angle(s_man_)) ./ cos(th)); % Reconstruction of the original signal in time domain
s_man_comp_f = fftshift(fft(s_man_comp)); % FT of the reconstructed signal
figure(1); hold on; plot(v_axis, db(abs(s_man_f_full)));
hold on; plot(v_axis, db(abs(s_man_comp_f)));
legend({'HD spectrum', 'Manipulated with cosine Spectrum', 'Compensated from Manipulated spectrum'}); grid on;