- #1
lilphy
- 28
- 0
Hello
I am studying for my exam and found an interesting exercise that I'm trying to solve
1. Homework Statement
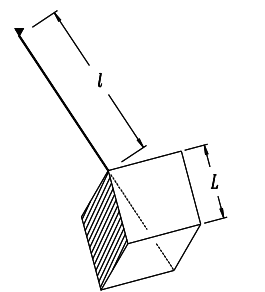
A pendulum consists of a thin rod of length ℓ and
mass m suspended from a pivot ∇ in the figure to the
right. The bob is a cube of side L and mass M, attached
to the rod so that the line of the rod extends through
the center of the cube, from one corner to the
diametrically opposite corner (dashed line).
.
(a) Locate the distance of the center of mass
from the point of support.
(b) Find the moment of inertia I of the (entire)
pendulum about the pivot point.
(Hint: obviously it is too hard to find the
moment of inertia of a uniform cube about an
arbitrary axis through its center of mass by
integrating directly, so there must be some simple trick…)
(c) Write down the equation of motion in terms of I and any
other relevant parameters.
(d) Find the frequency of small oscillations.
I don't know if this is correct :
a/ The center of mass of the cube is at a distance L√3/2 to the corner where the rod is fixed. So the distance between the two centers of mass is L√3/2+l/2.
So the center of mass of the whole system is at a distance m/(M+m)*(L√3/2+l/2) to the cube center of mass and at a distance d=m/(M+m)*(L√3/2+l/2) - L√3/2 to the corner ?
b/ For the moment of inertia of the cube about an axis through the cdm and a corner, I found that it is equal to the moment of inertia about an axis that passes through the center of mass and the center of one face =ML²/6 and for the rod about the corner I=ml²/3
so Itot=ml²/3+ML²/6
c/ If we take φ to be the angle made by the pendulum and the vertical (passes through the pivot) we have to use I*d²φ/dt²=τ with τ the torque
I don"t know what is the expression for the torque here considering that for this pendulum the rod has a mass ?
Thanks
I am studying for my exam and found an interesting exercise that I'm trying to solve
1. Homework Statement
A pendulum consists of a thin rod of length ℓ and
mass m suspended from a pivot ∇ in the figure to the
right. The bob is a cube of side L and mass M, attached
to the rod so that the line of the rod extends through
the center of the cube, from one corner to the
diametrically opposite corner (dashed line).
.
(a) Locate the distance of the center of mass
from the point of support.
(b) Find the moment of inertia I of the (entire)
pendulum about the pivot point.
(Hint: obviously it is too hard to find the
moment of inertia of a uniform cube about an
arbitrary axis through its center of mass by
integrating directly, so there must be some simple trick…)
(c) Write down the equation of motion in terms of I and any
other relevant parameters.
(d) Find the frequency of small oscillations.
Homework Equations
The Attempt at a Solution
I don't know if this is correct :
a/ The center of mass of the cube is at a distance L√3/2 to the corner where the rod is fixed. So the distance between the two centers of mass is L√3/2+l/2.
So the center of mass of the whole system is at a distance m/(M+m)*(L√3/2+l/2) to the cube center of mass and at a distance d=m/(M+m)*(L√3/2+l/2) - L√3/2 to the corner ?
b/ For the moment of inertia of the cube about an axis through the cdm and a corner, I found that it is equal to the moment of inertia about an axis that passes through the center of mass and the center of one face =ML²/6 and for the rod about the corner I=ml²/3
so Itot=ml²/3+ML²/6
c/ If we take φ to be the angle made by the pendulum and the vertical (passes through the pivot) we have to use I*d²φ/dt²=τ with τ the torque
I don"t know what is the expression for the torque here considering that for this pendulum the rod has a mass ?
Thanks