Discussion Overview
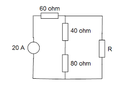
The discussion revolves around a current divider circuit problem, specifically focusing on calculating the resistance R in a circuit with multiple resistors. Participants are exploring the application of current division principles and addressing discrepancies between their calculations and textbook values.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant calculated the resistance R to be 720 ohms using a current divider equation but found a discrepancy with the textbook answer of 30 ohms.
- Another participant pointed out that the 60 Ω resistor is not in series with the 40 Ω and 80 Ω resistors, suggesting that the presence of resistor R affects the circuit configuration.
- A participant emphasized the need to correctly apply the current division expression, indicating that 20 A enters the node and must be divided between the parallel branches.
- One participant expressed confusion about the series combination of the 40 ohm and 80 ohm resistors and reiterated their calculation, which still resulted in a value for R that was too large.
- Another participant provided a general form of the current divider equations to clarify how to express the division of current between two parallel resistances.
Areas of Agreement / Disagreement
Participants do not appear to reach a consensus, as there are differing interpretations of the circuit configuration and the application of the current divider equation. Confusion remains regarding the calculations and the correct approach to finding R.
Contextual Notes
There are unresolved assumptions regarding the circuit layout and the application of the current divider formula. Participants have not fully clarified the relationships between the resistors involved.