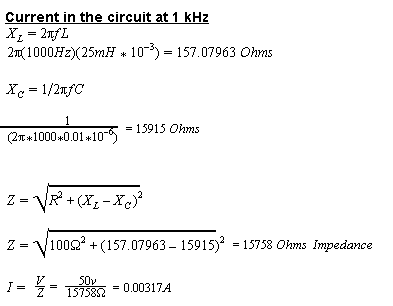SUMMARY
The discussion focuses on calculating the current in an RLC series circuit with specific components: a 100-ohm resistor, a 0.01uF capacitor, a 25mH inductor, and a 50V AC voltage source at 1kHz. Participants noted that the capacitor value significantly affects the impedance, which in turn influences the current calculation. The user expressed uncertainty about the capacitor value, indicating that verifying component specifications is crucial for accurate results.
PREREQUISITES
- Understanding of RLC circuit theory
- Familiarity with impedance calculations
- Knowledge of AC voltage sources
- Ability to interpret circuit components and their values
NEXT STEPS
- Research impedance in RLC circuits
- Learn how to calculate current using Ohm's Law in AC circuits
- Study the effects of component values on circuit behavior
- Explore simulation tools for RLC circuit analysis
USEFUL FOR
Electrical engineering students, hobbyists working with RLC circuits, and anyone involved in circuit design and analysis.