Linus Pauling
- 187
- 0
1.
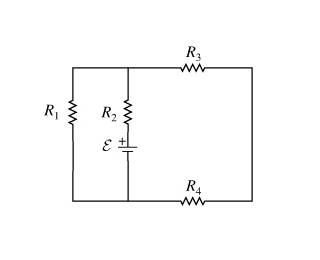
What is the current through each resistor
2. All the obvious stuff...
3. Ok, without showing all my work, here's what I have solved and know is right:
The equivalent resistance of the whole circuit is 56.3 ohm. From this, I used Ohm's law to get the equivalent current for the circuit, which is 0.213A.
Where I am stuck is now using this to get the individual currents for each resistor. For example, I calculated I_2 = V/R_2 = 12V/45ohm = 0.27A
Similarly, I found found the others, so here's what I got (which is incorrect):
I_1 = 0.8A
I_2 = 0.27
I_3 = 0.48
I_4 = 0.6
Also, I notice that these values sum to 2.12, which approximately euqals 2.13, which is the equivalent current with the decimal point moved over... where am I going wrong?
What is the current through each resistor
2. All the obvious stuff...
3. Ok, without showing all my work, here's what I have solved and know is right:
The equivalent resistance of the whole circuit is 56.3 ohm. From this, I used Ohm's law to get the equivalent current for the circuit, which is 0.213A.
Where I am stuck is now using this to get the individual currents for each resistor. For example, I calculated I_2 = V/R_2 = 12V/45ohm = 0.27A
Similarly, I found found the others, so here's what I got (which is incorrect):
I_1 = 0.8A
I_2 = 0.27
I_3 = 0.48
I_4 = 0.6
Also, I notice that these values sum to 2.12, which approximately euqals 2.13, which is the equivalent current with the decimal point moved over... where am I going wrong?