Sonderval
- 234
- 11
If I understand everything correctly, space near (but outside) a mass is curved negatively, so that if I create a triangle with, for example, rigid rods and the mass in its center, the angles would sum up to less than 180°. (If I am mistaken, please correct me.)
On the other hand, the typical light-bending pictures look like this
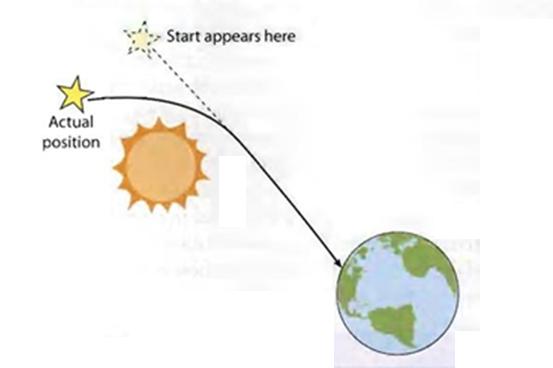
I do understand that the space projection of the iight geodesic does not coincide with the shortest path in space as gotten by laying out rods (this is obvious because there is a dt² in the formula for the space-time distance).
But how does the projection of the light geodesics look like, exactly? If I had three stars situated on a triangle with the mass in the middle, would the angular sum of the space projections of the geodesics be smaller or larger than 180°? From the fact that images are shifted away from the central mass, I would think that the sum has to be larger, but I'm not sure.
On the other hand, the typical light-bending pictures look like this
I do understand that the space projection of the iight geodesic does not coincide with the shortest path in space as gotten by laying out rods (this is obvious because there is a dt² in the formula for the space-time distance).
But how does the projection of the light geodesics look like, exactly? If I had three stars situated on a triangle with the mass in the middle, would the angular sum of the space projections of the geodesics be smaller or larger than 180°? From the fact that images are shifted away from the central mass, I would think that the sum has to be larger, but I'm not sure.