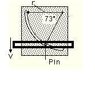
- #1
Kasthuri
- 17
- 0
Homework Statement
A pin is constrained to move in a circular slot of radius 39mm. At the same time a slotted bar also constrains the pin to move down with constant velocity 8mm/s. (as shown in attached diagram).
What is the magnitude of the acceleration of the pin for the position shown?
Homework Equations
NB: instead of using n&t as hinted as suggested, I used x and y coordinate system
The Attempt at a Solution
time taken for pin to move to position:
[39mm x sin(73)] / 8 mm/s = 4.6619... seconds
position of pin is:
x = 39 - sqrt(39^2 - 8^2*t^2)
so
x = 39 - sqrt(1521 - 64t^2)
y = -8t
pin's velocity is downward hence, it's acceleration is due to sideways movement: (x direction):
x^2 - 2*39*x = -64t^2 **
taking differential of **:
2*x*dx/dt - 2*39*dx/dt = -128t ***taking differential of ***:
2*dx/dt + 2x*d^2x/dt^2 - 2*39*d^2x/dt^2 = -128 ****
Now, substitute t=4.6613.. into ** to get x = 17.83... mm
then substitute x and t values into *** to get dx/dt = 14.0959... mm/s
then substitute dx/dt into **** to get d^2x/dt^2 = 2.05515...mm/s^2therefore,
answer: 2.055185 mm/s^2
However, my answer is wrong and I have no idea why?
thank you for any help you can give me
Last edited: