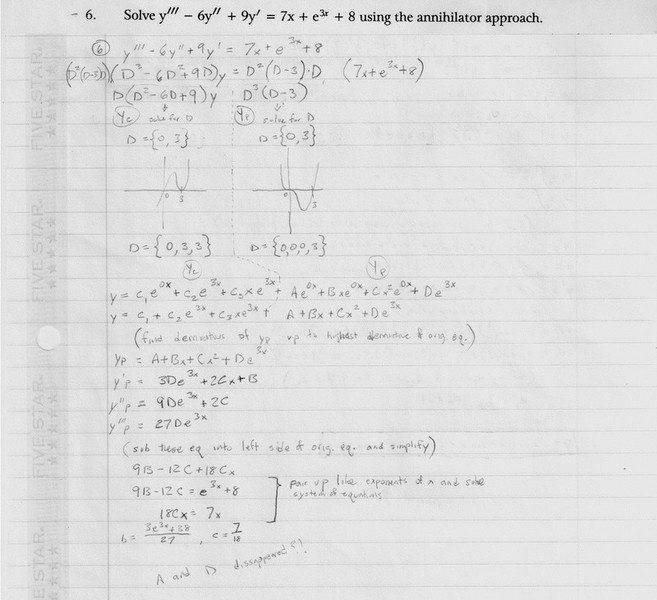D.E. Annihilator method question

[Jeff12341234]

When I solve for A,B,C, and D, A and D disappear. Is that ok? Are the terms that contained A and D simply omitted from the solution equation or have I made some other mistake somewhere?

 

[Mark44]

When I solve for A,B,C, and D, A and D disappear. Is that ok? Are the terms that contained A and D simply omitted from the solution equation or have I made some other mistake somewhere?

The complementary function, y_c = c₁ + c₂e^3x + c₂xe^3x. The particular solution can't have either of the last two functions, above. It has to have x²e^3x in it. The particular solution also can't have a pure constant in it, as you have with Ae^0x, which is really just A. It has to have x and x².

 

[Jeff12341234]

So where did I go wrong?
Which specific line or step is incorrect and what should it be?

 

[Mark44]

The first line that starts off "y = ..." You have too many terms in it. The particular solution should be y_p = Ax + Bx² + Cx²e^3x.

What you need to do is to apply enough annihilators to get to a homogeneous equation. That would be D³(D - 3)³y = 0.

The roots of the char. equation are {0, 0, 0, 3, 3, 3}. These would correspond to 1, x, x², e^3x, xe^3x, and x²e^3x.

The characteristic equation for the homogeneous version of the original DE has roots {0, 3, 3}, corresponding to 1, e^3x, and xe^3x. The particular solution can't have any of these three functions. It will have the others that are listed in the paragraph above this one.

 

[Jeff12341234]

yc, when expanded out, has a highest power of 3 so it has 3 roots; {0, 3, 3}. Right?
yp is to the 4th power when expanded out so doesn't it have to have 4 roots? {0, 0, 0, 3}?
Is that logic correct so far?

 

[Mark44]

yc, when expanded out, has a highest power of 3 so it has 3 roots; {0, 3, 3}. Right?
yp is to the 4th power when expanded out so doesn't it have to have 4 roots? {0, 0, 0, 3}?
Is that logic correct so far?

No, because of a mistake you made early on. The right side of your original DE is 8 + 7x + e^3x. The annihilator for it is D²(D - 3), not D²(D - 3)D = D³(D - 3) as you show. Note that D²(8 + 7x) = D(D(8 + 7x) = D(0 + 7) = 0. You have an extra factor of D.

The original equation, as a homogeneous DE is y''' - 6y'' + 9y' = 0, or (D³ - 6D² + 9D)y = 0. This can be written as D(D - 3)²y = 0.

The rootso of the char. equation are r = 0, and r = 3 (multiplicity 2). These roots correspond to, as I've already said, the functions {1, e^3x, xe^3x}.

In converting the origininal nonhomogeneous equation of order 3 to a homogeneous equation of order 6, you're appending two factors of D and one factor of D - 3. There are a lot of repeated roots there: r = 0 is of multiplicity 3 and r = 3 is of multiplicity 3 as well. The set of solutions are {1, e^3x, xe^3x[/color], x, x², x²e^3x[/color]}.

The first three in the set above (in blue) are a basis for y_c, which represents a basis for the solution of y''' - 6y'' + 9y' = 0. The second group of three (in green) are a basis for y_p, a particular solution of the nonhomogenous equation y''' - 6y'' + 9y' = 8 + 7x + e^3x. A function that is part of y_c CANNOT ALSO BE IN y_p, and that is what you are doing. You have 1 (= e^0x) in both y_c and y_p and you have e^3x in both, as well.

 

[Jeff12341234]

I understand what you're saying. I need to figure out why the initial mistake was made though. From what I understand:
7x = D^2
e^(3x) = (D-3)
8 = 8x^0 = D
When put together I get D^2*(D-3)*D. Which one of those is wrong?

 

[Mark44]

I understand what you're saying. I need to figure out why the initial mistake was made though. From what I understand:
7x = D^2
e^(3x) = (D-3)
8 = 8x^0 = D
When put together I get D^2*(D-3)*D. Which one of those is wrong?

You don't need (and shouldn't have) separate factors of D and D². D² annihilates A + Bx for any constants A and B.

D²(A + Bx) = D(D(Ax + B)) = D(A) = 0.