- #1
- 11,308
- 8,732
I am sharing this to brag about my former boss and mentor Lionel Barthold. He is well into his 90s, but his mind is so sharp that he continues with brilliant inventions. I'm very proud of him.
What would power level DC-DC transformers be good for?
The basic element is a "column" which is a collection of a large number of capacitors in series, with a bypass switch around each capacitor. Connect the column to the high voltage side and the capacitors charge up. Now disconnect the high voltage side (all switching is done at current zeroes), bypass some of the capacitors and connect the column to the low voltage side. But that's unstable, because on the next cycle the capacitors don't begin with equal initial charges. The solution is to choose different subsets of the capacitors for each half cycle. That is called the "sorting" solution for charge equalization. None of the capacitors ever get fully discharged. With a large number of capacitors to choose from, you can do a lot of smoothing. The switching frequency is as high as possible, limited by switching speeds. Also throw in a little L to charge resonantly.
I think it is very clever. All of us could solve the simple DC circuit for each half cycle. But the circuit configuration is changed 800 times per second. If we say that each of 500 capacitors can have 4 charge levels, and switching frequency is 400 hertz, then there are ##800*2^{500}*4^{500}## possible combinations per second. But ##4^N## is an overestimate because initial charges are not fully independent, they depend on the time history. Even so, the result is a very large number of switching+initial_condition configurations per second, well above ##10^{100}##. Some of the capacitors are redundant, allowing for failures.
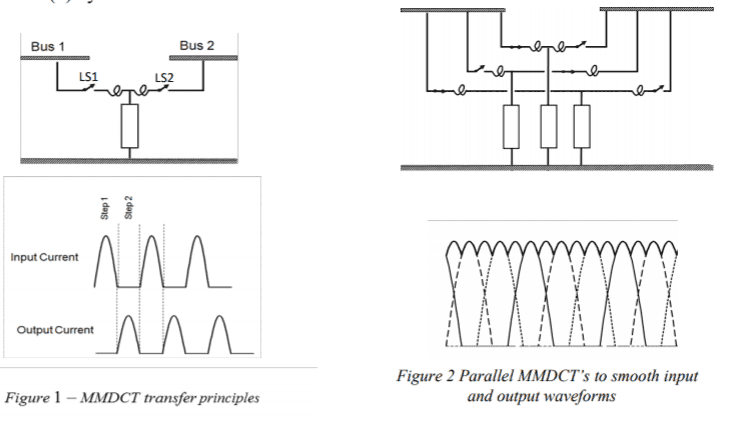
The scheme is shown below. One "column" on the left and with three parallel "columns" on the right. The three columns help smooth the current. (Don't get confused, this is not three phase power, it is three DC devices in parallel.)
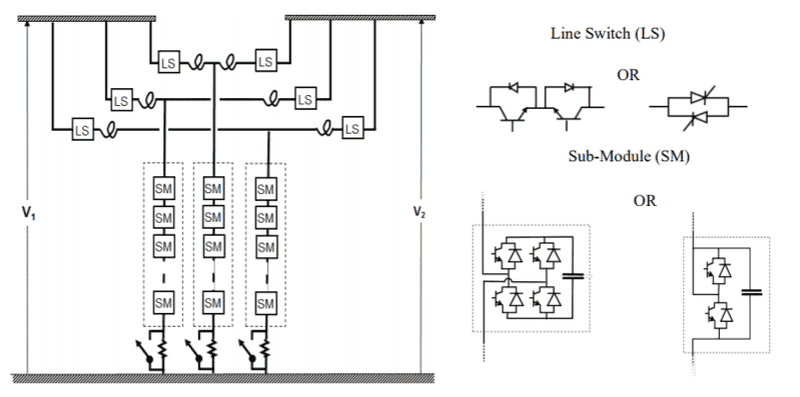
 Here's a schematic showing details of the switching electronics.
Here's a schematic showing details of the switching electronics.
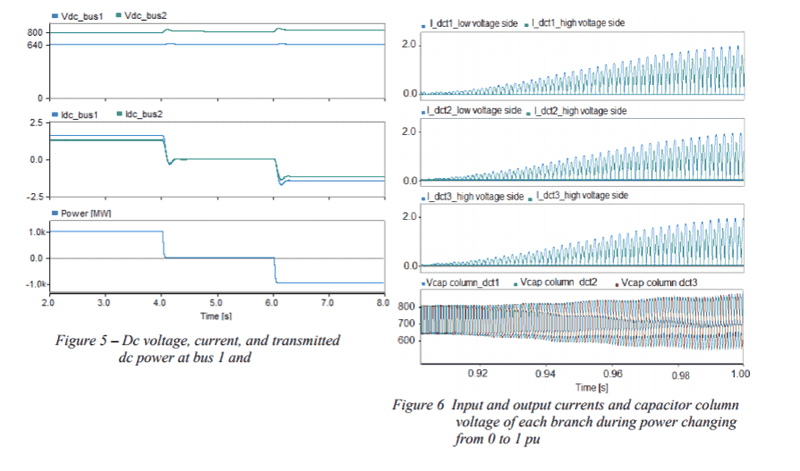
Here's a little simulation. We have a 640KV bus, 200 km of HVDC line, the transformer, another 200 km of line, and an 800 KV bus. The transformer has 400 submodules in each column. Switching frequency is 400 hertz.

The simulation shows a transient, +1000 MW transfer, zero MW, then -1000 MW, in only 6 seconds. demonstrating bidirectional power flow with the same bus voltages. The transients show below are at the transformer. The currents have an enormous amount of ripple, but it is high frequency. At the bus ends of the lines, the ripples are largely filtered out by the inductance and capacitance of the 200 km of line, so that the DC looks fairly smooth.
Just wanted to share. I think this stuff is cool.
What would power level DC-DC transformers be good for?
- Connecting different voltage level HVDC lines without conversion to AC.
- Direct connection of solar farms to HVDC without conversion to AC.
- Offshore wind farms are best connected to land with underwater HVDC cables. They can generate low voltage DC and connect to HVDC without conversion to AC.
The basic element is a "column" which is a collection of a large number of capacitors in series, with a bypass switch around each capacitor. Connect the column to the high voltage side and the capacitors charge up. Now disconnect the high voltage side (all switching is done at current zeroes), bypass some of the capacitors and connect the column to the low voltage side. But that's unstable, because on the next cycle the capacitors don't begin with equal initial charges. The solution is to choose different subsets of the capacitors for each half cycle. That is called the "sorting" solution for charge equalization. None of the capacitors ever get fully discharged. With a large number of capacitors to choose from, you can do a lot of smoothing. The switching frequency is as high as possible, limited by switching speeds. Also throw in a little L to charge resonantly.
I think it is very clever. All of us could solve the simple DC circuit for each half cycle. But the circuit configuration is changed 800 times per second. If we say that each of 500 capacitors can have 4 charge levels, and switching frequency is 400 hertz, then there are ##800*2^{500}*4^{500}## possible combinations per second. But ##4^N## is an overestimate because initial charges are not fully independent, they depend on the time history. Even so, the result is a very large number of switching+initial_condition configurations per second, well above ##10^{100}##. Some of the capacitors are redundant, allowing for failures.
The scheme is shown below. One "column" on the left and with three parallel "columns" on the right. The three columns help smooth the current. (Don't get confused, this is not three phase power, it is three DC devices in parallel.)
Here's a little simulation. We have a 640KV bus, 200 km of HVDC line, the transformer, another 200 km of line, and an 800 KV bus. The transformer has 400 submodules in each column. Switching frequency is 400 hertz.
The simulation shows a transient, +1000 MW transfer, zero MW, then -1000 MW, in only 6 seconds. demonstrating bidirectional power flow with the same bus voltages. The transients show below are at the transformer. The currents have an enormous amount of ripple, but it is high frequency. At the bus ends of the lines, the ripples are largely filtered out by the inductance and capacitance of the 200 km of line, so that the DC looks fairly smooth.
Just wanted to share. I think this stuff is cool.
Last edited: