CptXray
- 22
- 3
Homework Statement
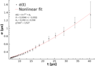
Hello, I have a problem with my data analysis from my lab. My goal is to find drift velocity of the electron and it's diffusion coefficient. The experiment looked like this: I've measured the time difference between signals on two gaseous detectors. The source of the signal were ##\alpha## particles from radioactive element inside the measurement system. Alpha particles ionize the gas inside chamber and then electrons are accelerated in a constant potential etc. Everything went fine until professor said that full width at half maximum should be ##\sigma = A \cdot t^{3/2} + \sigma_{0}## and it does match my data:
Homework Equations
The problem is that in general ##\sigma = \sqrt{2Dt}##.
The Attempt at a Solution
I don't know to go form ##\sqrt{2Dt}## to ##A\cdot t^{3/2} + \sigma_{0}##, because the last thing to do is finding diffusion coefficient. I'd appreciate any help and tips.