Definition of radius of sight optics

AI Thread Summary
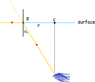
The discussion centers on the concept of the radius of sight for a fish submerged 3 meters underwater, focusing on how light refraction affects visibility. It explains that the fish can only see a circular region on the water's surface due to the refraction of light, which creates a limit defined by the critical angle of incidence. Total internal reflection prevents light from entering the fish's eye beyond this critical angle, thus restricting its view. The conversation suggests visualizing this with a light bulb analogy to trace light paths and understand the implications of Snell's law. Ultimately, the radius of sight is determined by the angles at which light can refract into the water and reach the fish's eye.
Werg22
Messages
1,431
Reaction score
1
"A fish is 3 meters underwater. What is the fish's sight radius of the external world?"

My question is what is the definition of this radius? What does it mean?
 
Physics news on Phys.org
If you consider the refraction of light entering the water, you'll realize that any light that makes it to the fish's eye must enter the water within a circle at the water's surface. Find the radius of that circle.
 
If you look up towards the surface from within a swimming pool you will find that a circular region appears on the surface of the pool where you can see what is outside of the pool. Outside of this circular region you cannot see what is above the surface. This circle is centered on a point right above you and its existence can be explained with total internal reflection.
 
I'm not sure if I understand (a quick drawing might be helpfull) but if I do, I have to calculate the distance between the fish and a point on the surface of the water where a ray that is parrallel to a straight line between the fish and that same point is not refracted?
 
A ray traveling from the eye of the fish to point p on the surface are incident at the surface of the ocean at the critical incident angle \alpha_c. Beyond this point total internal reflection will take place and rays cannot enter from above the surface into the eye of the fish.
 

Attachments

  • fish eye view.gif
    fish eye view.gif
    13.1 KB · Views: 492
andrevdh has provided a picture that will surely help, but I suggest you try the following to understand what's going on. Imagine the fish's head to be replaced by a light bulb emitting light in all directions. Trace the path of several of these rays as they refract into the air (apply Snell's law of refraction) and see what you can deduce. Start with rays that are nearly vertical (small angle of incidence) and then slowly increase the angle of incidence and see what happens to the refracted ray in air. You'll find, as andrevdh states, that after some critical angle of incidence the light from the bulb (on the fish's head) won't make it out of the water.

Then realize that the light coming from outside the water to the fish's eye must follow these same paths but in reverse.
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Previous university exam problem on refraction (that I think is wrong)
Replies
14
Views
4K
What is the internal radius of the optical fibre
Replies
2
Views
2K
What is the definition of Unit Optical Depth?
Replies
1
Views
1K
Contact Mechanics: Deformation of a ball on a surface
Replies
3
Views
1K
Geometric Optics: Find Fish Apparent Position & Length in Fishtank
Replies
6
Views
1K
General question about the definition of moment of force (Torque)
Replies
7
Views
796
Calculating Net Force on a Wheel: Magnitude and Direction | 0.350 m Radius
Replies
4
Views
2K
Calculating Archerfish's Line of Sight Angle in Relation to Squirt Angle
Replies
5
Views
4K
Critical angle: find the depth of the fish looking up
Replies
4
Views
3K
Could the Image from the First Mirror Be Real for the Second Mirror?
Replies
7
Views
2K

Hot Threads

Recent Insights

Back
Top