Delayed choice quantum eraser - partial information retrieval

[rnk]

In Delayed choice quantum eraser experiment (https://en.wikipedia.org/wiki/Delayed_choice_quantum_eraser) entangled photons are sent on different paths. They reach their detectors at different times. The one arriving early is called a signal photon. The photon that arrives at its destination at later time randomly goes through one of the available paths which constitutes (or not) a loss of information and then we either see (or not) interference like pattern or a pattern consistent with particle behavior. This behavior is mirrored by the signal photon.

This looks as if the information from one photon propagated backward in time. But even though information corresponding to future events is created before these events occur we cannot retrieve this information before the future events actually take place, because we see mix of different future states of the signal photon without ability to distinguish them. This is the understanding I have after reading the Wikipedia article.

Whilst I see why we may not retrieve this information with full accuracy I fail to understand why shouldn't we be able to retrieve a certain fraction of the information using the underlying probability density functions.

Knowing distributions behind these patterns:

the question is: can we retrieve non 100% but also non random quality (50%) information from these patterns about the future location of the entangled photon?

We can give our best estimate where the entangled photon is going to land given where the signal photon was detected. For example:

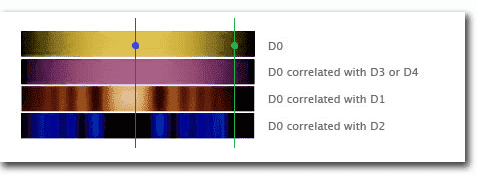
if the blue signal photon is detected then we can be quite certain that the entangled photon will land in D3, D4 or D1. Although, based on the color coding, D3 + D4 seems to be somewhat similar to D1 so it's not necessarily useful to us. On the other hand, if we detect the green signal photon we can expect that the entangled photon will most likely end up in D3 or D4 which is very informative. Is that correct?

 

[Strilanc]

The landing position does give you information, but not the kind you're hoping for. The landing position gives you information about the D1:D2 proportion, but it doesn't affect the (D1+D2):(D3+D4) proportion. That's the proportion you want to change (but can't in a useful way).

 

[entropy1]

As I understand it, (D1+D2)≅(D3+D4), meaning that the probability of being detected at D1 or D2 is roughly equal to the probability of being detected at D3 or D4, which means that detection is not more likely in D3+D4.