Delta and star transformation of AC circuits

[his_tonyness]

Homework Statement

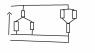
For the balanced three-phase loads shown in FIGURE 3,
ZY = (15 + j15) Ω and ZΔ = (45 + j45) Ω. Determine:
Uploaded file C1.png

(a) the equivalent single Δ-connected load,

(b) the equivalent single Y-connected load obtained from the Δ-Y transformation of (a) above,

(c) the equivalent single Y-connected load obtained by transforming the Δ sub-load of FIGURE 3 to a Y and with the star-points of the two Y-sub-circuits connected together,

(d) the total power consumed in case (a) above if the line voltage of the three-phase supply is 415 V at 50 Hz.

Homework Equations

The Attempt at a Solution

For (a) P=Q=R=(15+15i)
Star "PQR" --->Delta "ABC" equivelant =
A=PQ+QR+RP/R
Since the loads QPR are all the same value and same equation form then A=B=C, ((15+15i)*(15+15i)+(15+15i)*(15+15i)+(15+15i)*(15+15i))/(15+15i)=45+i45
Delta equivelant is A=45+i45, B=45+i45, C=45+i45

For(b) The reverse of (a) I assume; Delta ---> Star =
Q=AC/A+B+C
P=AB/A+B+C
R=BC/A+B+C

Q=P=R= 15+i15

Questions seems deceptively easy for my liking

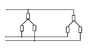
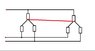
(c) Is the diagram C2.png how the transformation and two Y sub-circuit connected star points should look like?
I need a hint on how to form the equations for this if it is correct(im sure its obvious but I am not sure.)
Any help greatly appreciated.

 

[gneill]

For (a) they want a single Delta load. You've converted the Y to a Delta but now you have two Deltas as loads. Combine them into one.

For (b) they want you to take the single Delta from above and make a single Y.

Your diagram for part (c) doesn't make sense. You should have the single Delta that results from part (a) connected appropriately to the source. Having the line voltage and a Delta connection should make finding the power fairly straightforward... note how the individual impedances of the loads are connected to the sources.

 

[his_tonyness]

So do i need to combine two deltas using product over the sum rule in (a) and use that answer to make a Y transformation in(b)?

 

[gneill]

So do i need to combine two deltas using product over the sum rule in (a) and use that answer to make a Y transformation in(b)?

That's the idea. I think you'll find that finding the parallel impedances is greatly aided by the values chosen for the problem ;)

 

[his_tonyness]

(a)
((45 + j45) (45 + j45))/(90 + j90)
=22.5+j22.5 ohms

(b)
((22.5 + j22.5) (22.5 + j22.5))/((22.5 + j22.5) + (22.5 + j22.5) + (22.5 + j22.5))
=7.5+j7.5 ohms

Is question (c) essentially the product over the sum of ZY = (15 + j15) with the two Y three phase loads in parallel which is
((15 + j15) (15 + j15))/((15 + j15) + (15 + j15)) = 7.5+j7.5 ohms

For (d) The single delta load (22.5+j22.5), the power is basically (I^2)*R? It gives the frequency of 50Hz but I can't find a power equation or direct link for this. I know power factor depends on frequency and watts law uses power factor in its equation.

 

[gneill]

For (d) note that you are given the Line voltage. Note how Line voltage presents on the Δ load (there's an individual line voltage across each of the impedances). So you have potential difference and impedance for each. So you can calculate the current in a given impedance, right?

After that, what's the expression for complex power given the voltage V and current I?

 

[his_tonyness]

I=V/Z =9.2222-j9.2222 A , P = VI = 415*(9.2222-j9.2222)= 3827.22-j3827.22 watts.
Thats just for the single delta load in (a)

 

[gneill]

I=V/Z =9.2222-j9.2222 A , P = VI = 415*(9.2222-j9.2222)= 3827.22-j3827.22 watts.
Thats just for the single delta load in (a)

Okay, one thing. To compute the complex power you need to use the complex conjugate of the current in order make the power's angle work out with the correct sign (not that it's a big issue here where you just need the real component of the complex power). So the equation for the complex power is p = VI*, where I* represents the complex conjugate of I. The complex conjugate just changes the sign of the imaginary component.

So, you can pick out the real power dissipated by one of the impedances, right? What then is the total real power dissipated?

 

[his_tonyness]

The total real power is the sum of the single delta load (3827.22+j3827.22) watts and the three phase ZY load (415*13.833+j13.833= 5740.695+j5740.695i)

 

[gneill]

No, real power is real only. No imaginary part. Imaginary power dissipates no energy, as it's simply exchanged back and forth between the load and the power source over a cycle.

Now, didn't the single Delta load from part (a) represent the entire load? After all, you took the time to change the Y load to its Delta form and then combine it with the existing Delta, resulting in a "single Delta load", right? If you want to find the total power dissipated, then it makes sense to start with that single Delta load and find the power dissipated by one of its impedances, then scale to three of them...

 

[his_tonyness]

the real power dissapated in one of the impedances times 3 (3827.22*3)=11481.66 watts.

 

[gneill]

Yup. You might express it in kW and trim the significant figures a bit :)

 

[his_tonyness]

Well that seems simple enough! Thanks for your help once again.:)

 

[The_daddy_2012]

I don't understand the need to times by three again.

Line voltage = 415v
Therefore phase voltage = 239.6

239.6/22.5+j22.5 = 5.33+j5.33A

P=VI*

P= 240 x 5.33-j5.33

P=1279.2 -j1279.2

x3 because of the three phases.

3837.6-j3837.6 = total power

3837.6W is actual power.

Why is there a need to times by three again?

 

[gneill]

It's the line voltage, not the phase voltage that's impressed across the individual load impedances in the Delta configuration. By converting to phase voltage you've effectively divided by $\sqrt{3}$ twice when calculating the power. That's the same as dividing by three.

 

[dave pallamino]

isn't vl = vp on a delta network?

 

[gneill]

isn't vl = vp on a delta network?

Yes, if the source is a delta configured source. In this case the source is not specified and we're given only the line-to-line voltage.

 

[MrBondx]

For (a) they want a single Delta load. You've converted the Y to a Delta but now you have two Deltas as loads. Combine them into one.

For (b) they want you to take the single Delta from above and make a single Y.

Your diagram for part (c) doesn't make sense. You should have the single Delta that results from part (a) connected appropriately to the source. Having the line voltage and a Delta connection should make finding the power fairly straightforward... note how the individual impedances of the loads are connected to the sources.

Hie guys I'm still not getting part (c) even after reading this, in my calculation I transformed the delta of fig. 3 to a Y giving me 15 + j15 same as with the other Y.

'And with star-points of the two Y-sub-circuits connected together'
Does this part of the question change my calculation above ( well, if I calculated right)

 

[gneill]

Hie guys I'm still not getting part (c) even after reading this, in my calculation I transformed the delta of fig. 3 to a Y giving me 15 + j15 same as with the other Y.

'And with star-points of the two Y-sub-circuits connected together'
Does this part of the question change my calculation above ( well, if I calculated right)

No, it doesn't change your calculation. But your calculations aren't finished. You left off at the point where you have two Y-connected loads. You have yet to combine them into a single load.

 

[MrBondx]

No, it doesn't change your calculation. But your calculations aren't finished. You left off at the point where you have two Y-connected loads. You have yet to combine them into a single load.

Thanks gneill,

So if I combine them using product over sum I get 5+j5. Is that correct?

 

[MrBondx]

Thanks gneill,

So if I combine them using product over sum I get 5+j5. Is that correct?

just corrected an error. Now giving me 7.5 + j7.5

 

[gneill]

just corrected an error. Now giving me 7.5 + j7.5

That's better

 

[Hndstudent]

Hi gneill, for part d) i calculated my phase current to be 9.2222-j9.2222 A

so P= 3 x 415 x Iph = 11478.9 - j11478.9 Watts

im not confident that this is correct though?

thanks

 

[gneill]

It looks okay if you remember that power consumed is real power only.

When you calculate the complex power, use the complex conjugate of the current. That is, $P = V \cdot I^*$. This sorts out a certain sign issue that falls out during the derivation. Your text probably covers this.

 

[Hndstudent]

It looks okay if you remember that power consumed is real power only.

When you calculate the complex power, use the complex conjugate of the current. That is, $P = V \cdot I^*$. This sorts out a certain sign issue that falls out during the derivation. Your text probably covers this.

so it was, many books back. thanks for your help

 

[js3]

So do i need to combine two deltas using product over the sum rule in (a) and use that answer to make a Y transformation in(b)?

Hi, I'm just after a bit of help. I understand that gneill confirmed that using the product over sum is the correct technique to combine the two delta impedances, but in my textbook it quotes this as a Π to T transformation. Would anybody be able to shed a bit more light on this? Thanks

 

[gneill]

Hi, I'm just after a bit of help. I understand that gneill confirmed that using the product over sum is the correct technique to combine the two delta impedances, but in my textbook it quotes this as a Π to T transformation. Would anybody be able to shed a bit more light on this? Thanks

The original circuit had both Δ and a Y loads (Some call a Δ configuration a π configuration). The idea was to transform one of the loads to the same form as the other so that they could then be easily "summed" to a single load. That combined load could then be transformed as required.

Converting the Δ to a Y first leaves you with two Δ loads. They can be easily combined since the corresponding impedances are in parallel (hence the product over sum rule to combine them). The resulting single Δ can then be transformed to its Y equivalent as required.

 

[js3]

Thank you for your help on that, much clearer now. I have another question, I've been watching some tutorials and is converting a star impedance to it's equivalent delta impedance really as easy as multiplying by 3?

 

[gneill]

Thank you for your help on that, much clearer now. I have another question, I've been watching some tutorials and is converting a star impedance to it's equivalent delta impedance really as easy as multiplying by 3?

Yes, if all the impedances are identical.

 

[brenfox]

Hi, regarding question d. This is how I expressed my working out to get my answer (looking at the previous posts I now realize my answer is wrong but would like to know if my train of thought is correct)
Total impedance = 45+j45
Voltage = 415v
I =v/r* = 415(45-j45)/45+j45(45-j45)
= 18675-j18675/2025-j2025
total current = 9.2-j9.2 amps
P=vi*
P=415x(9.2-j9.2)
Real power = 3818watts. think I am supposed to times this by 3 but still not sure why(even after reading the posts!)

 

[gneill]

Hi, regarding question d. This is how I expressed my working out to get my answer (looking at the previous posts I now realize my answer is wrong but would like to know if my train of thought is correct)
Total impedance = 45+j45

In what way is that the "total impedance"? Total impedance of what?

 

[Spongecake]

For part C would the circuit look like this (see picture) before I make it into 1 single Y load.

 

[gneill]

For part C would the circuit look like this (see picture) before I make it into 1 single Y load.

Part C also specifies: "...and with the star-points of the two Y-sub-circuits connected together," What do you suppose is meant by that?

 

[Spongecake]

Would it be like this?

 

[gneill]

Would it be like this?

That would be my interpretation, yes.