SUMMARY
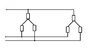
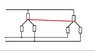
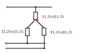
The forum discussion focuses on the transformation of AC circuit loads between Delta (Δ) and Wye (Y) configurations, specifically for balanced three-phase loads with impedances ZY = (15 + j15) Ω and ZΔ = (45 + j45) Ω. The participants detail the calculations for obtaining equivalent single loads through Δ-Y transformations and discuss the total power consumed when the line voltage is 415 V at 50 Hz. Key insights include the use of the product-over-sum rule for combining impedances and the importance of using the complex conjugate of current when calculating complex power.
PREREQUISITES
- Understanding of three-phase AC circuits
- Knowledge of Delta (Δ) and Wye (Y) transformations
- Familiarity with complex impedance and power calculations
- Ability to apply the product-over-sum rule for impedance combinations
NEXT STEPS
- Study the principles of three-phase power systems
- Learn about complex power calculations in AC circuits
- Explore advanced topics in impedance transformation techniques
- Review practical applications of Delta and Wye configurations in electrical engineering
USEFUL FOR
Electrical engineering students, circuit designers, and professionals working with three-phase AC systems who need to understand load transformations and power calculations.