Derivation of Mutual Inductance Energy

[yosimba2000]

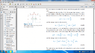
I've attached a picture of my book.
So there is a figure of two inductors mutually connected.

The book says that initially, current 1 and current 2 are zero. Then when current 1 goes from 0 to I1, the energy stored in circuit is only the energy in inductor 1. <-- This is my question, but please read further.

Then it says keep I1 constant, and move current 2 from 0 to I2. The increase in energy from this is now from energy stored in inductor 2 and also the mutual energy in inductor 1, due to changing current 2 from 0 to I2.

So total energy is now Energy of Inductor 1 + Energy of Inductor 2 + Mutual Energy in Inductor 1.

But my question is... if changing current 2 from 0 to I2 resulted in mutual energy change in inductor 1, then wouldn't have bringing current 1 from 0 to I1 also have resulted in mutual energy change in inductor 2?

So then total energy would be
Energy of Inductor 1 + Energy of Inductor 2 + Mutual Energy in Inductor 1 + Mutual Energy in Inductor 2?

 

[Tom.G]

The problem states that current I2 is zero when I1 is applied. Since there is no current in L2 at that time there is no energy to store in L2.
Stored energy is proportional to Inductance times squared Current.

 

[Babadag]

I agree with Tom. Since the energy is the integrated power from 0 to t and the power is p2= v*i2 if i2=0[ no current will be in L2 from 0 to t1] than p2=0 all the time .From t1 to t2 the i1 is constant and only i2 will rise from 0 to i2 then in L2 the stored energy will be L2*i2^2/2 and another energy part will be added to w1 [M12*i1*i2].

 

[yosimba2000]

The problem states that current I2 is zero when I1 is applied. Since there is no current in L2 at that time there is no energy to store in L2.
Stored energy is proportional to Inductance times squared Current.

But how can current I2 be zero if current 1 goes from 0 to I1?
Physics says if they are coupled, then there must be some induced EMF when current 1 increases, hence there should be nonzero current in inductor 2.

I don't see how you can just say it is zero...

 

[Babadag]

If it is d.c. current and the current will rise very slowly then no change of current i1 or i2 will occur by induction phenomenon.

Let's say the increasing part of i1 it will be Di1=M12*(di2/dt)/ZL1 that means Di1=K*di2/dt .

Representing i2 variation curve in two dimensions diagram di2/dt=tan(alpha).

One can increase the current i2 very slowly then alpha could be almost 0.

 

[Tom.G]

There will be a VOLTAGE induced in coil2 that depends on the number of turns and the rate of change of I1. The current I2 will be zero if there is nothing connected to coil2, no circuit for the current to flow in, no load.

 

[yosimba2000]

So then this power being described in the book is only for a special situation in which we assume Inductor 2 is initally NOT coupled with Inductor 1.
But then Inductor 2 is coupled AFTER Current 1 has reached steady state?

 

[Tom.G]

Not necessarily. If there is no coupling then there won't be any voltage induced in coil2 at the time i1 increases. If there is coupling, coil2 has an induced voltage. In either instance coil2 has no effect on the circuit because there is no current flow in coil2. That is the key. There has to be current flow in coil2 for it to affect the circuit.

If you then connect a battery across coil2, then that current flowing thru coil2 creates its own magnetic field. It's the total magnetic field that does the actual energy storage, and also does the coupling between the two coils.

 

[yosimba2000]

Not necessarily. If there is no coupling then there won't be any voltage induced in coil2 at the time i1 increases. If there is coupling, coil2 has an induced voltage. In either instance coil2 has no effect on the circuit because there is no current flow in coil2. That is the key. There has to be current flow in coil2 for it to affect the circuit.

If you then connect a battery across coil2, then that current flowing thru coil2 creates its own magnetic field. It's the total magnetic field that does the actual energy storage, and also does the coupling between the two coils.

Wait, won't the induced voltage generate a current in coil 2?

 

[Tom.G]

We must note the difference between a Voltage and a Current. Try thinking of a flashlight. The batteries may last several years if the flashlight is never used. Leave the flashlight turned on and the batteries will die in a matter of hours. When the flashlight is turned off the batteries still have voltage. When turned on, there is current flowing thru the bulb, draining the batteries.

A similar thing applies to your circuit. Coil2 serves as the batteries. Since the terminals of coil2 are not connected to anything else, it's as if the flashlight is turned off, no light bulb connected. There can be a voltage induced in coil2 but there is no place for any current to flow.

An analogy some people find useful is a water hose. You can consider the water pressure to be voltage and the amount of water flowing thru the hose to be current. Turning off the nozzle is like turning off a switch, nothing flows.

Or in an electrical circuit the voltage is how hard the electrons are trying to get away from each other and the current is how many are actually getting away.

 

[yosimba2000]

Hmm... then you're saying this power formula initially assumes Coil 2 is coupled, but is not wired to ground? And after Coil 1 has reached steady state, Coil 2 is the attached to ground and causes current to flow?

 

[Tom.G]

Well, not exactly. There is voltage induced in Coil2 only while the current in Coil1 is CHANGING. At steady state, by definition, there is no change in current, hence there is no longer any voltage induced in Coil2.

 

[yosimba2000]

Well, not exactly. There is voltage induced in Coil2 only while the current in Coil1 is CHANGING. At steady state, by definition, there is no change in current, hence there is no longer any voltage induced in Coil2.

If the bolded is true, then I still don't understand why the energy formula initially assumes no current in Coil 2 as current in Coil 1 increases. I mean, it says current in Coil 2 is zero while current in Coil 1 increases, but they don't say why. Changing current in Coil 1 MUST induce current in Coil 2 if the coils are coupled. So if there is induced current in Coil 2, there must be an induced voltage in Coil 2. And Power in Coil 2 during that time must be P = IV, hence there shoud be energy in Coil 2.

 

[Tom.G]

Changing current in Coil 1 MUST induce current in Coil 2 if the coils are coupled.

Nope. Changing current in Coil1 induces a VOLTAGE in Coil2. There is not a load on Coil2 so there is no place for current to flow. For current to flow there must be a path from the voltage source (Coil2 in this case), thru a load, and back the the other terminal of the voltage source (the two ends of Coil2).

See my post #10, above.

 

[yosimba2000]

Ok, so then if the voltage is induced in coil 2, but current is zero as current in coil 1 rises, then the formula assumes the load in coil 2 isn't connected until after coil 1 is steady state?

I'm sorry, this is really confusing me...

 

[Tom.G]

That's right. In fact your book states exactly that in the paragraph between Eq. (13.25) and (13.26).

 

[yosimba2000]

I see the book says about keeping current in coil 2 as zero, but nothing about attaching a load after coil 1 has reached steady state. Unless it's implied? :/

 

[Tom.G]

The "load" is the current I2.

The way I have been discussing it so far is that Coil2 was operating as a source. Which it was while I1 was increasing. This was to highlight the lack of current flowing in Coil2 during that time.

Now we are considering Coil2 as an input to the magnetic circuit because I2 has started to flow from an external current source. Just as I1 started previously.