Derivation of waveguide condition for two light rays

[loginorsinup]

How did they derive equation (6)?

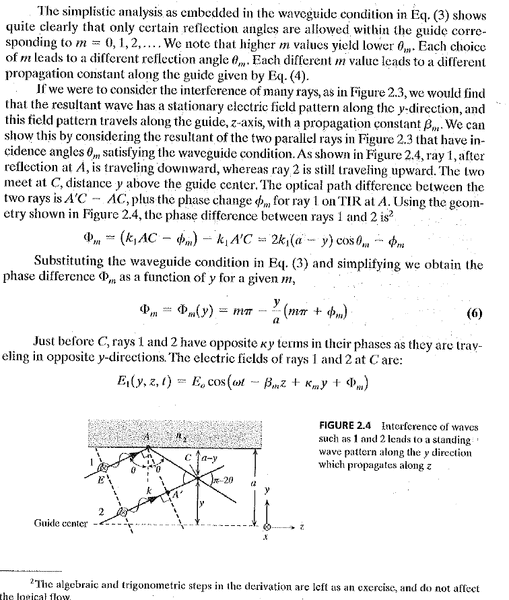
I don't like how they say -Φ_m instead of Φ_m, but that aside, I get that both rays 1A and 2A' travel the same distance, but AC incurs a phase change due to total internal reflection (-Φ_m) and it travels AC from there. Meanwhile, A'C is the distance the other ray travels. So the difference between these two is what sets the phase difference between the two.

Somehow, they made AC - A'C = 2*(a-y)*cos(θ_m) it seems. I should note that the angle that is split into two by the perpendicular line (really an arrow) is 2θ, so the angle by A, C, and the interface is θ. Beyond that, I don't really know how to approach this. They conveniently said it is left as an exercise for the reader, but that always seems like laziness to me. It's not clear to me where it came from and I've spent several hours trying to "get it."

 

[Greg Bernhardt]

Thanks for the post! Sorry you aren't generating responses at the moment. Do you have any further information, come to any new conclusions or is it possible to reword the post?

 

[loginorsinup]

I haven't figured this out since I posted, no. I'm still curious where this came from. It's not actually relevant to the rest of the chapter. I think somehow (a-y) might be a hypotenuse? But I don't see it.

 

[Plant_Boy]

What is Equation (3)?