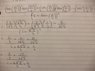- #1
thatguythere
- 91
- 0
Homework Statement
d/dx(sec(x)/1+tan(x)
Evaluate at x=∏/6
Homework Equations
The Attempt at a Solution
((1/cos(x))(1+tan(x))-(sec(x))(sin(x)/cos(x)))/(1+tan(x))^2
((1/cos(x))-(sec(x))(sin(x)/cos(x)))/(1+tan(x))
I used the quotient rule and reduced what I could. Have I done this right and can I go any further before evaluating? Thank you.