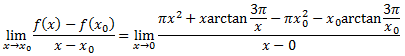- #1
goody1
- 16
- 0
Hello everybody, could you help me with this problem please? I have to find a derivative in x0 of this function (without using L'Hospital's rule):
View attachment 9694
I used the definition View attachment 9695, but I don't know what to do next. Thank you.
View attachment 9694
I used the definition View attachment 9695, but I don't know what to do next. Thank you.