- #1
physics604
- 92
- 2
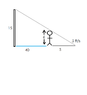
1. A street light is mounted at the top of a 15-ft-tall pole. A man 6 ft tall walks away from the pole with a speed of 5 fts along a straight path. How fast is the tip of his shadow moving when
he is 40 ft from the pole?
$$x^2+y^2=z^2$$
I've drawn a diagram so far (I've attached it to this thread), but I don't know where to start. Can someone give me a hint?
he is 40 ft from the pole?
Homework Equations
$$x^2+y^2=z^2$$
The Attempt at a Solution
I've drawn a diagram so far (I've attached it to this thread), but I don't know where to start. Can someone give me a hint?