SUMMARY
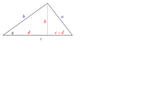
The discussion focuses on deriving a generalized formula for the variable d in relation to c-d with respect to the angle θ in a right triangle. It establishes that when θ = 0, b equals c, and when θ = 90, d equals 0, indicating that d is the projection of b. The participants seek to clarify the relationship between these variables using trigonometric functions to express the ratio of d over b.
PREREQUISITES
- Understanding of trigonometric functions and their applications in geometry
- Familiarity with right triangle properties and relationships
- Knowledge of angle measurement in degrees
- Basic algebra for manipulating equations and ratios
NEXT STEPS
- Research the sine and cosine functions to understand their role in triangle projections
- Explore the derivation of trigonometric identities relevant to right triangles
- Study the concept of angle projections in geometry
- Learn about the Law of Sines and its applications in triangle calculations
USEFUL FOR
Mathematicians, geometry students, and anyone interested in trigonometric applications in right triangles.