Derive the Maxwell "with source" equation

[LCSphysicist]

Homework Statement

.

Relevant Equations

.

We need to derive the Maxwell "with source" equation, of course, using the tensor equation $$\partial F^{\mu v}/ \partial x^{v} = j^{\mu}/c$$

D is the spacetime dimension
To do this, it was said to us vary the action wrt the $A^{\mu}$

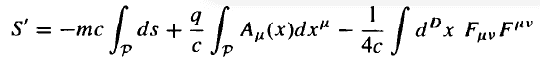
The first term just vanish, and I want to evaluate the third term.
$$\frac{-1}{4c} \int d^{D}x (\partial_{\mu} \delta A_{v} - \partial_{v} \delta A_{\mu})(\partial^{\mu} \delta A^{v} - \partial^{v} \delta A^{\mu})$$
$$\frac{-1}{4c} \int d^{D}x 2((\partial_{\mu} \delta A_{v})(\partial^{\mu} \delta A^{v}) - (\partial_{\mu} \delta A_{v})(\partial^{v} \delta A^{\mu})$$
$$\frac{-1}{2c} \int d^{D}x (\partial_{\mu} \delta A_{v}) \delta F^{\mu v} *$$

After that equation, the things get pretty messy... My attempt was to find somewhere a way to apply the divergence theorem and get the flux, after that i would get the charge density and so the current, but i was not able to do that

OBS: in * i am considering that $\partial \delta A = \delta \partial A$, but i am not sure 'bout that.

 

[vanhees71]

That's fine, because you don't vary the space-time arguments $x$ in Hamilton's principle. However you wrote some $\delta$ too much. Note that $\delta (F_{\mu \nu} F^{\mu \nu})=2 F_{\mu \nu} \delta F^{\mu \nu}=4 F_{\mu \nu} \delta \partial^{\mu} A^{\nu}$ and now go on in calculating the variation such to make the integrand $\propto \delta A^{\nu}$.

For the 2nd term, I'd write it out in explicit form. Also think about, how $j^{\mu}(x)$ looks for a single point particle!