Deriving an expression from geometry

[Levi Tate]

Homework Statement

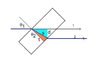
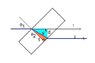
I need to derive an expression for the displacement of light as a function of thickness of glass and the angles.

I will post a screen shot of the formula to be derived but it can also be found here

http://clas.wayne.edu/multimedia/usercontent/File/Physics%20and%20Astronomy/Labs/PHY5341/Lab4%20Brewsters%20Angle.pdf

(pg 3)

Homework Equations

The equation is given as the solution. I am not very good with geometry so I don't really even know where to begin.

The Attempt at a Solution

Using Snell's law,

n1sinθ1=n2sinθ2

Solving for θ2 = Arcsin[(n1/n2)sinθ1]

So then I just have θ2.

Help, please?

 

[ehild]

See attachment. You have to find the expression for the distance (d) between the original ray (1) and the displaced one (2). t is the thickness of the slab. There are two right triangles in the picture, with common hypotenuse (s ). Find s in terms of t and θ₂, find d in terms of s and θ₂-θ₁. Eliminate θ₂.

ehild

 

[Levi Tate]

Thanks a lot for your help mate. I tried this problem for about an hour and I'm completely stuck. I never went to high school to get that Euclidian intuition and I'm dyslexic so I don't have a good geometric intuition. I'm just stuck, I can't see the solution in sight.

But I thank you for your assistance very much.

 

[ehild]

Do you see the right triangles in the picture? What is the relation between t, s and θ2?

What is the angle of the blue triangle between side s and the hypotenuse?


ehild