A Deriving Expression for Differentiation and Summation in Special Case

mahmud_dbm
Messages
17
Reaction score
0
Dear Friends

So, i have this special case where i have to do a differentiation and summation.
Please check the following.

upload_2016-12-27_1-2-7-png.110813.png


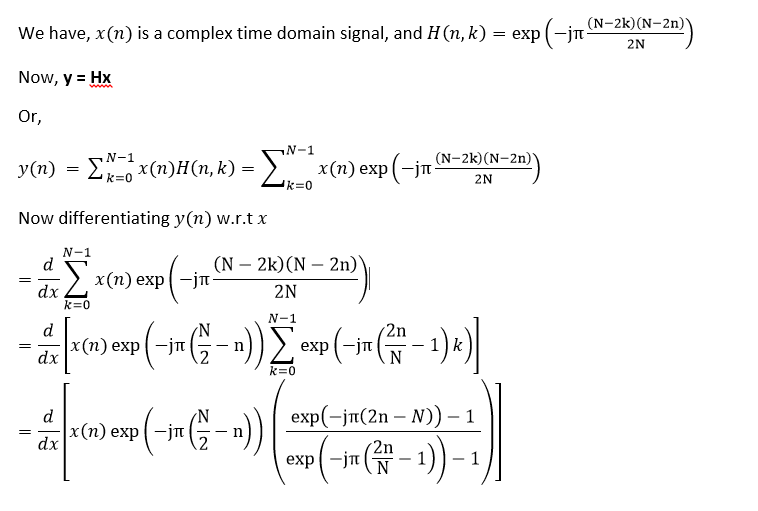
Is it okay ?? Or, i how should i proceed with this ?
 
Mathematics news on Phys.org
ok, what you did in the bracket were algebraic operations and the use of the formula for geometric series ##\sum_{k=0}^{N-1}t^{k}=\frac{t^{N}-1}{t-1}## where ##k=e^{-j\pi(2n/N-1)}##, now you must derive the expression respect ##\chi## ...
 

Thread 'What Exactly is Dirac’s Delta Function? - Insight'

Insights auto threads is broken atm, so I'm manually creating these for new Insight articles. In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/ by...
View full post »

Thread 'Fermat's Last Theorem'

Fermat's Last Theorem has long been one of the most famous mathematical problems, and is now one of the most famous theorems. It simply states that the equation $$ a^n+b^n=c^n $$ has no solutions with positive integers if ##n>2.## It was named after Pierre de Fermat (1607-1665). The problem itself stems from the book Arithmetica by Diophantus of Alexandria. It gained popularity because Fermat noted in his copy "Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et...
View full post »

Thread 'Useless continued fraction for 1'

I'm interested to know whether the equation $$1 = 2 - \frac{1}{2 - \frac{1}{2 - \cdots}}$$ is true or not. It can be shown easily that if the continued fraction converges, it cannot converge to anything else than 1. It seems that if the continued fraction converges, the convergence is very slow. The apparent slowness of the convergence makes it difficult to estimate the presence of true convergence numerically. At the moment I don't know whether this converges or not.
View full post »

Similar threads

I How Can Nested Summation Functions Be Simplified or Reversed?
Replies
6
Views
2K
B A summation that "feeds back into itself"
Replies
1
Views
1K
I Classifying Series Summation $$ \sum_{i=0}^{n} 2^{2^i} ~ ?$$
Replies
3
Views
1K
Newtons Divided Difference First Derivative
Replies
3
Views
1K
I Manipulate this summation with Exp
Replies
9
Views
1K
I Change of variables clarification
Replies
5
Views
1K
I Why is Griffiths Treating the Summation Like This?
Replies
4
Views
391
Maximizing Summation of F_t*R: Partial Derivative w.r.t R
Replies
1
Views
1K
MHB Basic symbology for involving a series but without summation necessarily
Replies
1
Views
2K
I Why did I lose 60% on my proof of Generalized Vandermonde's Identity?
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top