Igor Oliveira
- 2
- 0
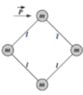
Homework Statement
Four equal discs of mass
Answer: The center of mass moves with constant velocity
Homework Equations
Linear momentum:
Angular momentum:
Impulse-momentum theorem:
The Attempt at a Solution
I obtained the first result by assuming that the the linear momentum transmitted by the impulse will be divided into four chunks, which will be associated with each mass. Then, the center of mass will notably move with velocity
(This problem was found in a textbook written in portuguese, so the translation might not be the best. Please comment any doubt with the problem statement!)
Attachments
-
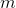 png.png234 bytes · Views: 730
png.png234 bytes · Views: 730 -
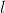 png.png201 bytes · Views: 772
png.png201 bytes · Views: 772 -
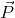 png.png246 bytes · Views: 444
png.png246 bytes · Views: 444 -
 file.png1.9 KB · Views: 453
file.png1.9 KB · Views: 453 -
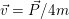 4m.png437 bytes · Views: 427
4m.png437 bytes · Views: 427 -
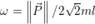 2%5Csqrt%7B2%7Dml.png585 bytes · Views: 443
2%5Csqrt%7B2%7Dml.png585 bytes · Views: 443 -
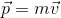 png.png363 bytes · Views: 455
png.png363 bytes · Views: 455 -
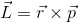 png.png407 bytes · Views: 417
png.png407 bytes · Views: 417 -
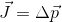 png.png361 bytes · Views: 439
png.png361 bytes · Views: 439 -
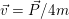 4m.png437 bytes · Views: 445
4m.png437 bytes · Views: 445 -
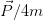 4m.png386 bytes · Views: 465
4m.png386 bytes · Views: 465