Engineering Designing a circuit from a transfer function

[izelkay]

Homework Statement

Homework Equations

The Attempt at a Solution

So I know how to derive a transfer function from a given circuit, but not how to design a circuit from a transfer function like the one above. It seems like there's a huge amount of possible solutions and I don't know where to begin in trying to come up with one other than guessing and checking (which would take a lot of time that I don't have on exams). Is there a systematic method or a particular approach to solve problems like this?

 

[LvW]

Yes - you are right, there are several possible circuit topologies. And - of course - many different impedance niveaus.
But, I think, you have selected a good and simple structure, which works in priciple.
However, I am afraid some values are not quite correct.
I suppose you know about the superposition rule, which allows you to separately find the various values by setting all but one signal sources to zero?

Questions: Why 4R2 between both opamps? Recalculate this value and - as a consequence - the time constant R1*C.

 

[NascentOxygen]

Once you remove the (+) input from ground, as you show for the second op-amp, then the (-) input is no longer a virtual earth. Have you analyzed that second op-amp arrangement to confirm the proportion of v₃ in v_o will be precisely what you hope it will be?

 

[izelkay]

Hey guys, thanks for your replies. I forgot to mention in my post that that solution isn't actually mine. It's my professors and I kind of just assumed it was right without checking it. It's problem 3 on this past exam:
http://www.ece.tamu.edu/~spalermo/ecen325/exam1_spring2014.pdf

If I use superposition with V1 only:

Vo = sR1CV1

V2 only:
1st op-amps output is grounded and v3 is grounded so the 2nd op amp behaves like an inverting amplifier:
Vo = -(4R2/4R2)V2
Vo = -V2

V3 only:
Vo = (1+(4R2/4R2||R2)) * V3 * (R/2R)
Vo = (1+5)V3(1/2)
Vo = 3V3So Vo = sR1CV1 - V2 + 3V3

If I did that correctly then this circuit really isn't a solution because it's missing the -4 in front of the V2 right?

 

[LvW]

If I did that correctly then this circuit really isn't a solution because it's missing the -4 in front of the V2 right?

Yes - that`s the error. Therefore, I did recommend to recalculate this resistor betwen the opamps.

 

[izelkay]

Yes - that`s the error. Therefore, I did recommend to recalculate this resistor between the opamps.

Hm okay since I didn't come up with this particular circuit I'm going to try and start from scratch since I'm probably going to have to do this on the coming exam.

Using two op-amps as a general template:
Start with V1 on the first op-amp, and because there's an "s" there's probably a capacitor. Since it's positive and I'm using two op-amps, V1 should go into the inverting terminal of the first op amp and then into the inverting terminal of the second op amp.

With V2 and V3 on the second op-amp, since V2 has a "-4" attached to it it will go into the inverting terminal of the second op-amp while V3 will go into the non-inverting terminal.

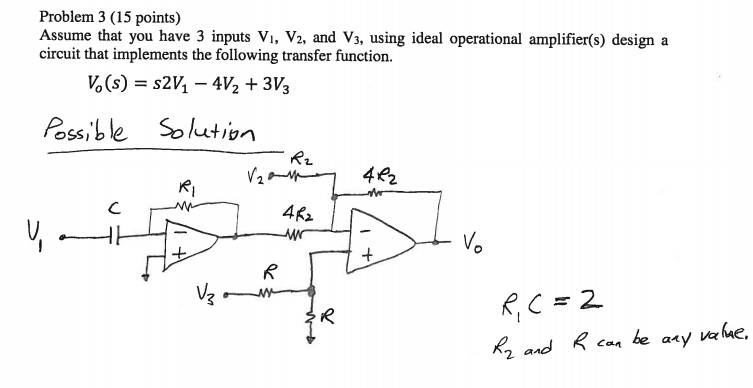
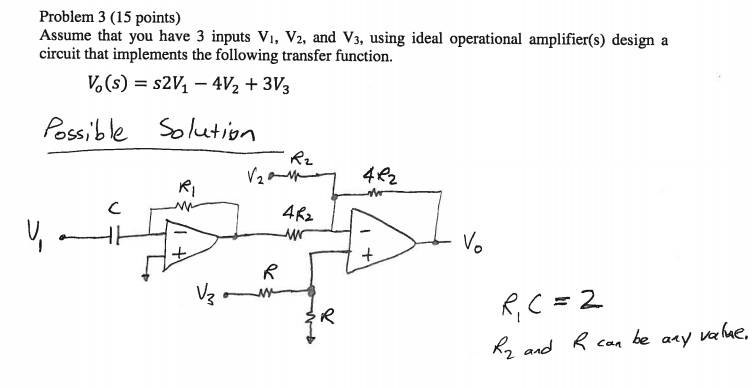
Now it's just a matter of picking components. This is what I came up with:

My reasoning:
V1 only:

Vo = s(R3/R2)R1CV1

V2 only:

Vo = -(R3/R2)V2

V3 only:

Vo = [1+(R3/R2)][R4R5/(R4+R5)]V3

Looking at V2, R3 has to equal 4 R2 to get -4 in front of V2.

Looking at V1, since R3 = 4R2, R1C = 1/2 to get 2s in front of V1

Looking at V3, since R3 = 4R2, The parallel connection of R4 and R5 has to equal 3/5 to cancel out the 5 from (1+(R3/R2)) and get the 3 in front of the R3:
R4R5 = 3
R4+R5 = 5

∴ R4 = 3/R5

3/R5 + R5 = 5

R5² - 5R5 + 3 = 0

This will have two solutions, and I picked the one where R5 = 4.3, so then R4 = 0.7 (exact values included in figure).

Would this be a valid solution?

 

[NascentOxygen]

Is there a resistor missing for v2? As drawn the (-) input is firmly fixed at v2.

 

[izelkay]

Is there a resistor missing for v2? As drawn the (-) input is firmly fixed at v2.

I made it similar to the first solution's circuit:

where the Vo for V2 here is -(4R2/4R2) = -V2
the resistor connected to V2 didn't matter here so I thought I didn't need it in my solution.
Was that incorrect to assume?

 

[izelkay]

Wait now that I'm looking at it again maybe I didn't calculate V2 only correctly in the original solution.

For this circuit

Shouldn't V2 only be:

Vo = -[4R2 / (4R2||R2) ]*V2

= -[4R2 / 4R2R2/5R2]*V2

= -[4R2*5R2/4R2*R2]*V2

= -(20/4)V2

= -5V2

If so I'll be back later to work on my solution some more

 

[izelkay]

Okay here's my new solution:

I connected a resistor to V2

V1 only is still the same relation:

Vo = s(R3/R2)R1*C*V1

V2 only is now:

Vo = -[R3(R6+R2)/(R6R2)] * V2

V3 only is now:

(1 + [R3(R6+R2)/(R6R2)]) * [(R4R5)/(R4+R5)] * V3

If I make R3/R2 = 2, then R1*C must equal 1 to satisfy the first part.

Then, R2 = R6 = 1, and R3 = 2 to satisfy the second part

Then R4 and R5 are the same as I had them before.

Is this solution correct?

 

[LvW]

Sorry - it is not. Strat with R3/R2=4

 

[LvW]

Sorry - read start /instead of strat).

 

[izelkay]

Sorry - it is not. Strat with R3/R2=4

If I make R3/R2 = 4 that would cause problems for my V2 term wouldn't it?

If R3/R2 = 4:

For V2, -[R3(R6+R2)/(R6R2)] * V2 becomes

-[4(R6+R2)/R6]V2

To make this -4V2,
R6 = 1
R2 = 0
which can't be

Also sorry but could you show me what's wrong with my solution? Did I mess up on the math somewhere?

 

[LvW]

For amplification of V2 you only need R3 and R6 (R2 is grounded).

 

[izelkay]

For amplification of V2 you only need R3 and R6 (R2 is grounded).

Ahh okay, thanks. I think I get the general gist of it now, I just need to be careful with the connections.