Determinant of vector of AXB for 3-D

[dpa]

Hi all,

This is a beginning step in proving aXb=|a||b|sin(theta)

thank you

 

[DonAntonio]

Hi all,

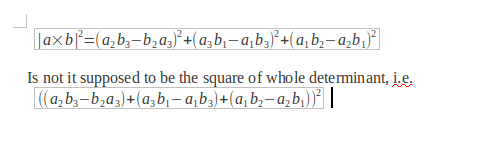
This is a beginning step in proving aXb=|a||b|sin(theta)

thank you

Assuming that expression with a's is the determinant, then yes: it must be the whole thing squared.

DonAntonio

 

[dpa]

I am talking abou this proof:

Thank You.

 

[chiro]

Hey dpa.

These brackets refer to the norm and the norm of a vector in R^n is simply is the sum of the components squared. [This norm is simply the ||x-0|| for some vector x]

Also you can't use this to prove what AXB is, but you can prove that for some directional normal vector n^{^} then you can prove that AXB = n^hat*length where length is |AXB|.

 

[dpa]

Thank You.