Determinants and Standard Orientation

jakey · Mar 20, 2010

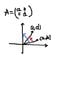
How do we show that, given a matrix $A$, the sign of the determinant is positive or negative depending on the orientation of the rows of A, with respect to the standard orientation of $R^n$?

quasar987 · Mar 20, 2010

Isn't that the very definition of "the rows making up the columns of A have the same (res. the opposite) orientation as the standard basis" ?

If not, write the definition of orientation. you're using.

jakey · Mar 20, 2010

quasar987 said: ↑

Isn't that the very definition of "the rows making up the columns of A have the same (res. the opposite) orientation as the standard basis" ?

If not, write the definition of orientation. you're using.

If you refer to the attached file, this matix has a positive orientation (and the sign of the determinant is positive) since the direction from (a,b) to (c,d) is counterclockwise, which is the same orientation as R2 (counterclockwise). Thanks!

quasar987 · Mar 20, 2010

I was asking that you write out the definition of what it means for a basis of R^2 to have the same (resp. the opposite) orientation as another basis of R^2.

Your little drawing with arrows does not constitute a mathematical definition.

Log in or Sign up

Determinants and Standard Orientation

jakey

quasar987

jakey

Attached Files:

pic1.jpg

quasar987