Determine the maximum ratio h/b

[Sanchayan Dutta]

Determine the maximum ratio $$h/b$$ for which the homogenous block will slide without toppling under the action of force F.The coefficient of static friction between the block and the incline is $$\mu_s$$.

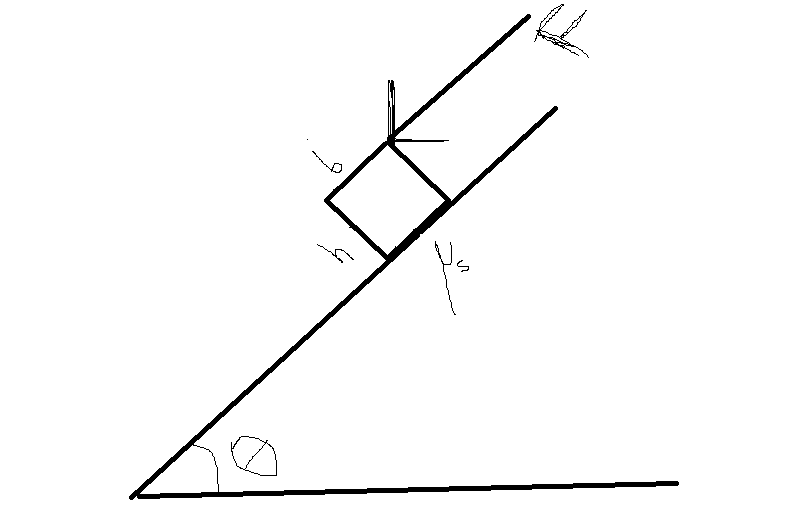
I have a doubt.About which point should the rotational equilibrium be applied?Should it be applied about centre of mass?Or should it be applied about the vertex opposite to the vertex where F is applied?Why?

**MY ATTEMPT:**

**Translational Equations**
$$F+mg\sin(\theta) \geq \mu N$$
and $$N=mgcos(\theta)$$

**Rotational Equations**
This is where I'm facing a problem.Depending upon which point the equilibrium is applied the required ratio will be obtained.

**MY VIEWS:**

Rotational equilibrium should hold at all points if no toppling/rotation happens.However the answer varies depending on the point of application of equilibrium.Strange.

 

[haruspex]

However the answer varies depending on the point of application of equilibrium.Strange.

You are right that it would be strange. As long as you take all relevant forces into account properly, you should get the same answer. You must be making a mistake in one or other of your attempts.
Please post those attempts.