- #1
annas425
- 17
- 0
Given the transfer function G(s) = 1 / (s(s+1)(s^2 + 4s + 13)), how would I determine the range of the values of K>0 such that the closed-loop poles are in the left-hand plane?
Picture of block diagram with transfer function:
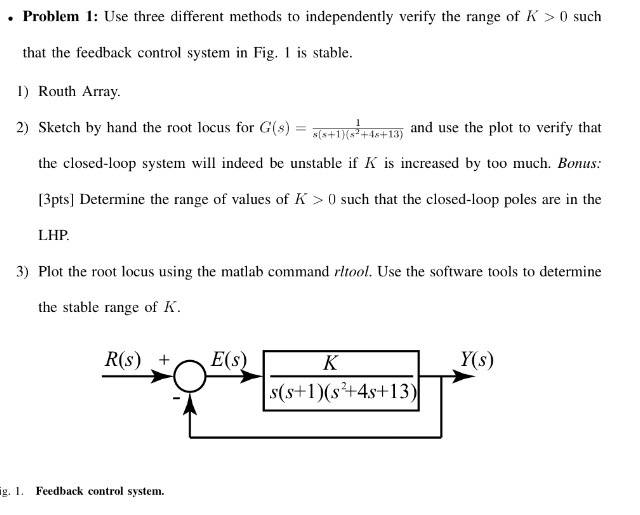
Not sure if this is right at all, but I know that a system is stable when K>0, so if the poles were to be in the left-hand plane (i.e., be stable), would it just be for all K>0? I am assuming it's more involved than just that, so I would really appreciate some help please! :)
Thank you in advance!
Picture of block diagram with transfer function:
Not sure if this is right at all, but I know that a system is stable when K>0, so if the poles were to be in the left-hand plane (i.e., be stable), would it just be for all K>0? I am assuming it's more involved than just that, so I would really appreciate some help please! :)
Thank you in advance!